《2025年作业本江西教育出版社七年级数学上册北师大版》

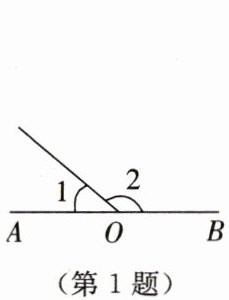
1. 如图所示，点 $ O $ 在直线 $ AB $ 上，若 $ \angle 1 = 40^{\circ} $，则 $ \angle 2 = $140°。

答案： 140°

2. 如图所示，已知 $ \angle EOA = 90^{\circ} $，射线 $ OD $ 在北偏东 $ 35^{\circ} $ 的方向，反向延长射线 $ OD $ 至点 $ C $，则 $ \angle DOE = $35°，$ \angle AOC = $55°。

答案： 35°
55°

3. 小亮利用星期日做社会调查，早晨 $ 9:00 $ 出发，中午 $ 12:30 $ 到家。小亮出发时和到家时时钟的时针和分针的夹角分别为90°和165°。

答案： 90°
165°

4. 换算。
(1)$ 1.36^{\circ} = $1$ ^{\circ} $21$ ' $36$ '' $；
(2)$ 41^{\circ}18'36'' = $41.31$ ^{\circ} $。

答案： 1
21
36
41.31

5. 如图所示，将三个同样的正方形的一个顶点重合放置。若 $ \angle 1 = 50^{\circ} $，$ \angle 3 = 30^{\circ} $，则 $ \angle 2 $ 的大小是10°。

答案： 10°

6. $ 9 $ 时 $ 20 $ 分时，时钟上时针与分针的夹角 $ \alpha $ 等于多少度？

答案： 解：$​α=(9-4)×30°+30°×\frac {20}{60}= 160°​$

7. 利用下图完成练习。
（1）写出所有能用一个字母表示的角。
（2）写出所有以点 $ A $ 为顶点的角。
（3）图中共有几个小于平角的角？

答案： 解：​
(1)∠B，​​∠C。​
​
(2)∠BAD，​​∠BAC，​​∠DAC。​
​
(3)7​个。

8. 如图所示，在 $ \angle AOB $ 的内部引 $ 1 $ 条射线，能组成多少个角？引 $ 2 $ 条射线，能组成多少个角？引 $ 3 $ 条射线呢？引 $ 5 $ 条射线呢？引 $ n $ 条射线呢？

答案： 解：$​1+2+3+…+(n+1)=\frac {(n+1)(n+2)}{2}​$
引​1​条射线能组成​3​个角；引​2​条射线能
组成​6​个角；引​3​条射线能组成​10​个角；
引​5​条射线能组成​21​个角；引​n​条射线
能组成$​\frac {(n+1)(n+2)}{2}​$个角。