《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 下列计算正确的是③④(填序号)。
①$(-1)× (-2)× (-3)=6$；
②$(-36)÷ (-9)=-4$；
③$\frac {2}{3}× (-\frac {9}{4})÷ (-1)=\frac {3}{2}$；
④$(-4)÷ \frac {1}{2}× (-2)=16$。

答案： ③④

2. 若a，b互为相反数，c，d互为倒数，$m^{2}=25，$则$3m+\frac {a+b}{3cd}=$15或-15。

答案： 15或-15

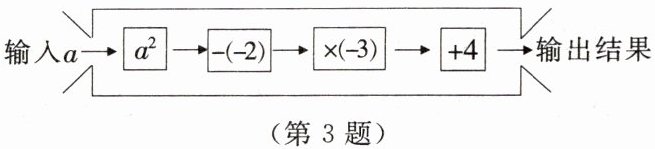
3. 下图是一个计算程序，若输入$a$的值为$-1$，则输出的结果应为-5。

答案： -5

4. 计算。
（1）$-1^{2}-(1-\frac {1}{2})÷ 3× (-7)$；
（2）$-(-2)^{2}-(-3)^{3}× \frac {1}{6}$。

答案： 解：原式$​=-1 - \frac {1}{2} \div 3 ×(-7)​$
$​                =-1 - \frac {1}{2} ×\frac {1}{3} ×(-7)​$
$​                =-1 + \frac {7}{6}​$
$​                =\frac {1}{6}​$
解：原式$​=-4 - (-27) ×\frac {1}{6}​$
$​                =-4 + \frac {9}{2}​$
$​                =\frac {1}{2}​$

5. 对于非零有理数$a$，$b$，规定$a\otimes b=\frac {a}{b}-1$。求$(-2)\otimes [(-3)\otimes (-4)]$的值。

答案： 解：原式$​=(-2)⊗(\frac {-3}{-4} - 1)​$
$​                =(-2)⊗(\frac {3}{4} - 1)​$
$​                =(-2)⊗(-\frac {1}{4})​$
$​                =\frac {-2}{-\frac {1}{4}} - 1​$
​                =8 - 1​
​                =7​

6. 有四个有理数$3$，$4$，$-6$，$10$，根据“$24$点”游戏规则，请你写出两个不同的算式，使其计算结果等于$24$。

答案： 解：​
(1)[10 + (-6) + 4]×3​
​
(2)(10 - 4)×3 - (-6)​