《2025年作业本江西教育出版社七年级数学上册北师大版》

1. 给出下列代数式：① $a + 1$；② $-\frac{3ab}{7}$；③ $5$；④ $-2a + 5b$；⑤ $a$；⑥ $\frac{1}{a}$。其中单项式有3个。

答案： 3

2. 单项式 $-\frac{\pi x^{3}y^{2}}{5}$ 的系数是$-\frac{\pi}{5}$，次数是5。

答案： $-\frac{\pi}{5}$
5

3. (1)在多项式 $3x^{2}y - x^{2} - 2y + 2$ 中，次数最高项的系数是3。
(2)多项式 $-3x^{3}y - 1 + 2xy^{2} - y^{3}$ 按照 $y$ 的降幂排列为$-y^{3} + 2xy^{2} - 3x^{3}y - 1$。

答案： 3
$-y^3 + 2xy^2 - 3x^3 y - 1$

4. 定义：若一个多项式有两项且两项的次数相同，则称这样的多项式为“齐次二项式”。若关于 $a$，$b$ 的多项式 $-2a^{m}b^{3} + na^{3}b^{2}$ 是“齐次二项式”，在数轴上表示 $n$ 的点在表示 $-2$ 的点的右侧距离 $5$ 个单位长度处，则 $m^{n} =$8。

答案： 8

5. 若单项式 $-\frac{1}{8}a^{2}b^{m}$ 与 $-\frac{3}{7}x^{3}y^{4}$ 是次数相同的单项式，则 $m$ 的值为5。

答案： 5

6. 已知关于 $x$ 的多项式 $(a + b)x^{5} + (a - 3)x^{3} - 2(b + 2)x^{2} + 2ax + 1$ 不含 $x^{3}$ 和 $x^{2}$ 项，则当 $x = -1$ 时，这个多项式的值为-6。

答案： -6

7. 指出下列代数式中的单项式、多项式和整式。
$2\pi x^{2}$，$\frac{1}{x}$，$-5$，$a$，$\frac{\pi}{2}$，$0$，$\frac{m + n}{2}$，$1 - \frac{1}{a}$，$3ab - 2a - 1$。

答案： 解：单项式：$​2\pi x^2，$-5，a，$\frac {\pi }{2}，$0；​ 
多项式：$​\frac {m+n}{2}，$3ab - 2a - 1；​ 
整式：$​2\pi x^2，$-5，a，$\frac {\pi }{2}，$0，$\frac {m+n}{2}，$​
​3ab - 2a - 1​

8. 某超市在国庆期间对商品实行优惠活动，规定如下：

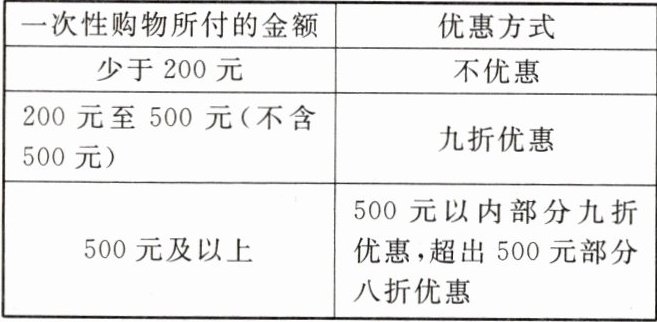
（1）若顾客在该超市一次性购物 $x(x\geq500)$ 元，实际付款 $y$ 元，请用含 $x$ 的代数式表示 $y$。
（2）某顾客两次购物的商品总金额共 $820$ 元，其中第一次购物的商品金额为 $a(200 ＜ a ＜ 300)$ 元，用含 $a$ 的代数式表示该顾客两次购物的实际付款总额。

答案： 解：​
(1)y = 500×0.9 + (x - 500)×0.8 ​
​= 0.8x + 50​
​
(2)​根据题意，得
​0.9a + 0.8×(820 - a - 500) + 500×0.9 ​
​= (0.1a + 706)​元