《2025年配套综合练习甘肃九年级数学上册华师大版》

化简：$ \sqrt{-a^{3}} $.


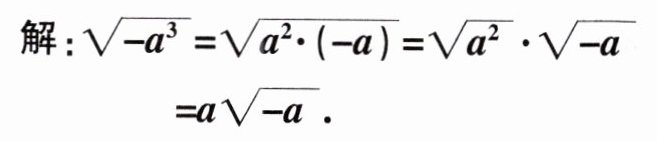
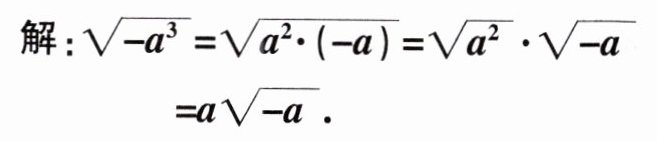
(1)错因：未讨论a的取值,直接应用$\sqrt{a^{2}}=a$化简,出现错误.
(2)纠错：根据二次根式有意义的条件得$-a^{3}≥0,\therefore a≤0.$∴原式=$\sqrt{a^{2}}\cdot\sqrt{-a}=|a|\sqrt{-a}=-a\sqrt{-a}$.

答案：
(1)未讨论a的取值,直接应用$\sqrt{a^{2}}=a$化简,出现错误
(2)根据二次根式有意义的条件得$-a^{3}≥0,\therefore a≤0.$
∴原式=$\sqrt{a^{2}}\cdot\sqrt{-a}=|a|\sqrt{-a}=-a\sqrt{-a}$

1. $\frac{\sqrt{4}}{\sqrt{9}}=$$\frac{2}{3}$,$\sqrt{\frac{4}{9}}=$$\frac{2}{3}$.
即$\frac{\sqrt{4}}{\sqrt{9}}$=$\sqrt{\frac{4}{9}}$.

答案： $\frac{2}{3}$ $\frac{2}{3}$ =

2. $\frac{\sqrt{49}}{\sqrt{100}}=$$\frac{7}{10}$,$\sqrt{\frac{49}{100}}=$$\frac{7}{10}$.
即$\frac{\sqrt{49}}{\sqrt{100}}$=$\sqrt{\frac{49}{100}}$.
试用含有字母$a,b$的式子表示上述规律：$\frac{\sqrt{a}}{\sqrt{b}}=$$\sqrt{\frac{a}{b}}$($a\geq0$,$b＞0$)①
即两个算术平方根的商,等于它们被开方数的商的算术平方根.

答案： $\frac{7}{10}$ $\frac{7}{10}$ = $\sqrt{\frac{a}{b}}$ $a\geq0$ $b＞0$ 商的算术平方根

二、商的算术平方根
将等式①左右两边的式子互换,得$\sqrt{\frac{a}{b}} = $$\frac{\sqrt{a}}{\sqrt{b}}$($a \geq 0,b ＞ 0$)
即商的算术平方根等于被除式的算术平方根除以除式的算术平方根.

答案： $\frac{\sqrt{a}}{\sqrt{b}}$ 除以

三、分母有理化
将分母中的根号化去的过程.

答案： 化去

四、最简二次根式
满足下面两个条件的二次根式叫最简二次根式.
1. 被开方数中不含分母.
2. 被开方数中所有因数(或因式)的幂的指数都小于2.

答案： 1.分母 2.小于2

小题快练
(打“√”或“×”)
1. $\sqrt{\frac{-4}{-9}} = \frac{\sqrt{-4}}{\sqrt{-9}}$.(×)
2. $\sqrt{\frac{3}{2}} = \frac{1}{2}\sqrt{3}$.(×)
3. $\sqrt{4a^{2} + 9b^{2}}$是最简二次根式.(√)
4. $\sqrt{0.5}$是最简二次根式.(×)

答案： 1.× 2.× 3.√ 4.×

【示范题 1】计算：(1)$\frac{\sqrt{72}}{\sqrt{6}}$=$2\sqrt{3}$.
(2)$\sqrt{1\frac{1}{2}} ÷ \sqrt{\frac{1}{6}}$=$3$.
【思路点拨】(1)直接运用$\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$($a \geq 0,b ＞ 0$)进行计算.
(2)先把带分数化成假分数,再运用除法法则计算.

答案：
(1)
$\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$（$a\geq0,b ＞ 0$），则$\frac{\sqrt{72}}{\sqrt{6}}=\sqrt{\frac{72}{6}}=\sqrt{12}=\sqrt{4×3}=2\sqrt{3}$。
(2)
$1\frac{1}{2}=\frac{3}{2}$，$\sqrt{1\frac{1}{2}}÷\sqrt{\frac{1}{6}}=\sqrt{\frac{3}{2}}÷\sqrt{\frac{1}{6}}=\sqrt{\frac{3}{2}÷\frac{1}{6}}=\sqrt{\frac{3}{2}×6}=\sqrt{9}=3$。
综上，答案依次为：
(1)$2\sqrt{3}$；
(2)$3$。