《2025年配套综合练习甘肃九年级数学上册华师大版》

一、位似图形、位似中心
两个图形的对应点$A与A'$,$B与B'$,$C与C'$,……,的连线都交于一点O,并且$\frac{OA'}{OA}$=$\frac{OB'}{OB}$=$\frac{OC'}{OC}$=…=k,这两个图形叫做位似图形.点O叫做位似中心.

答案： 交于一点O $\frac{OA'}{OA}$ $\frac{OB'}{OB}$ $\frac{OC'}{OC}$ 点O

二、位似的作用
利用位似的方法,可以把一个多边形放大或缩小.

答案： 放大 缩小

小题快练
(打“√”或“×”)
1. 位似图形是相似图形.(√)
2. 相似图形是位似图形.(×)
3. 位似图形的位似中心只有一个.(√)
4. 位似图形中的任意一对对应点到位似中心的距离之比等于相似比.(√)

答案： 1.√ 2.× 3.√ 4.√

【示范题】如图,在$6× 8$的网格图中,每个小正方形边长均为$1$,点$O和\triangle ABC$的顶点均为小正方形的顶点.

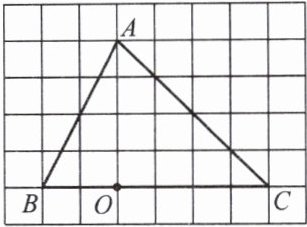
(1)以$O$为位似中心,在网格图中作$\triangle A'B'C'$,使$\triangle A'B'C'和\triangle ABC$位似,且相似比为$1:2$.
(2)连结(1)中的$AA'$,求四边形$AA'C'C$的周长.(结果保留根号)
【思路点拨】(1) 根据相似比是$1:2$,可知$A'$,$B'$,$C'分别是OA$,$OB$,$OC$的中点.
(2)根据勾股定理求出$AC$,$A'C'$的长,由于$AA'$,$CC'$的长易得,相加即可求得四边形$AA'C'C$的周长.

答案：
【解答】
(1) ①连结$OA$,取$OA的中点A'$,取$OB的中点B'$,取$OC的中点C'$；②连结$A'B'$,$A'C'$,则$\triangle A'B'C'$即为所求.
如图所示：

(2)$AA' = CC' = 2$,
在$Rt\triangle OA'C'$中,$OA' = OC' = 2$,
$\therefore A'C' = \sqrt{OA'^{2} + OC'^{2}} = \sqrt{2^{2} + 2^{2}} = 2\sqrt{2}$；
在$Rt\triangle OAC$中,$OA = OC = 4$,
$\therefore AC = \sqrt{OA^{2} + OC^{2}} = \sqrt{4^{2} + 4^{2}} = 4\sqrt{2}$,
$\therefore四边形AA'C'C$的周长
$= AA' + A'C' + C'C + AC$
$= 2 + 2\sqrt{2} + 2 + 4\sqrt{2} = 4 + 6\sqrt{2}$.