《2025年配套综合练习甘肃九年级数学上册华师大版》

1. 如图,点 A,B,C,D 的坐标分别是(1,7),(1,1),(4,1),(6,1),以 C,D,E 为顶点的三角形与△ABC 相似,则点 E 的坐标不可能是 (B)

A.(6,0)
B.(6,3)
C.(6,5)
D.(4,2)

答案： B

2. 下列条件中,能判定△ABC 与△DEF 相似的有 (B)
①∠A = 45°,AB = 12,AC = 15,∠D = 45°,DE = 16,DF = 40；
②AB = 12,BC = 9,∠A = 45°,DE = 20,EF = 15,∠D = 45°；
③∠A = 47°,AB = 15,AC = 20,∠E = 47°,DE = 28,EF = 21.
A.0 个
B.1 个
C.2 个
D.3 个

答案： B

3. 在△ABC 和△A'B'C'中,若∠B = ∠B',AB = 12,BC = 16,B'C' = 8,则 A'B' = 6时,△ABC ∽ △A'B'C'.

答案： 6

4. 如图,(1)若$\frac{OA}{OB} = $$\frac{OC}{OD}$,则△OAC ∽ △OBD.
(2)若∠B = ∠A,则△OAC ∽ △OBD.
(3)请你再写一个条件：∠C=∠D(或AC//BD),使△OAC ∽ △OBD.

答案：
(1)$\frac{OC}{OD}$；
(2)∠A；
(3)∠C=∠D(或AC//BD)

5. 已知点 P 是边长为 4 的正方形 ABCD 内一点,且 PB = 3,BF ⊥ BP,垂足是点 B,若在射线 BF 上找一点 M,使以点 B,M,C 为顶点的三角形与△ABP 相似(不含全等),求 BM 的长.

答案： $\frac{16}{3}$

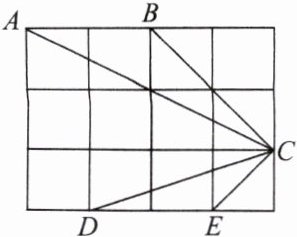
6. 如图,在 3×4 的正方形方格中,△ABC 和△DEC 的顶点都在边长为 1 的小正方形的顶点上.
(1)填空：∠ABC = 135°,BC = 2$\sqrt{2}$.
(2)判断△ABC 与△DEC 是否相似,并证明你的结论.

(2)相似.
∵BC=$\sqrt{2^{2}+2^{2}}$=2$\sqrt{2}$, EC=$\sqrt{1+1}$=$\sqrt{2}$,
∴$\frac{AB}{CE}=\frac{2}{\sqrt{2}}=\sqrt{2}$, $\frac{BC}{DE}=\frac{2\sqrt{2}}{2}=\sqrt{2}$,
∴$\frac{AB}{CE}=\frac{BC}{DE}$. 又∠ABC=∠CED=135°,
∴△ABC∽△CED.

答案：
(1)135；2$\sqrt{2}$；
(2)相似.
∵BC=$\sqrt{2^{2}+2^{2}}$=2$\sqrt{2}$, EC=$\sqrt{1+1}$=$\sqrt{2}$,
∴$\frac{AB}{CE}=\frac{2}{\sqrt{2}}=\sqrt{2}$, $\frac{BC}{DE}=\frac{2\sqrt{2}}{2}=\sqrt{2}$,
∴$\frac{AB}{CE}=\frac{BC}{DE}$. 又∠ABC=∠CED=135°,
∴△ABC∽△CED.