《2025年配套综合练习甘肃九年级数学上册华师大版》

如图,在 $\triangle ABC$ 中,$\angle ACB= 90^{\circ}$,$CD$ 为高,$\angle A= 30^{\circ}$,若 $BD= 3cm$,求 $AD$ 的长。

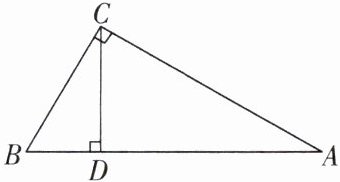
解：$\because \angle ACB= 90^{\circ}$,$\angle A= 30^{\circ}$,
$\therefore \angle B= 90^{\circ}-\angle A= 90^{\circ}-30^{\circ}=60^{\circ}$,$\angle BCD= 30^{\circ}$ ①
$\therefore BD= \frac{1}{2}DC$,即 $DC= 2BD= 2× 3= 6(cm)$ ②
在 $\triangle ADC$ 中,$\angle ADC= 90^{\circ}$,$\angle A= 30^{\circ}$,
$\therefore DC= \frac{1}{2}AD$,即 $AD= 2DC= 2× 6= 12(cm)$ ③
(1)找错：从第②步开始出现错误。
(2)纠错：在Rt△ABC中,∵CD是斜边上的高,∴∠BCD=∠A=30°,∴BC=2BD=6,∵∠ACB=90°,∠A=30°,∴AB=2CB=12(cm),∴AD=AB - BD=12 - 3=9(cm)

答案：
(1)②
(2)在Rt△ABC中,
∵CD是斜边上的高,
∴∠BCD=∠A=30°,
∴BC=2BD=6,
∵∠ACB=90°,∠A=30°,
∴AB=2CB=12(cm),
∴AD=AB - BD=12 - 3=9(cm)

一、锐角三角函数的概念
锐角三角函数
sinA cosA tanA

答案： sinA cosA tanA

二、锐角三角函数的性质
1. 0＜ $\sin A$ ＜1,0＜ $\cos A$ ＜1。
2. $\sin^2 A + \cos^2 A = $1。

答案： 1.0 1 0 1 2.1

三、特殊角的三角函数值

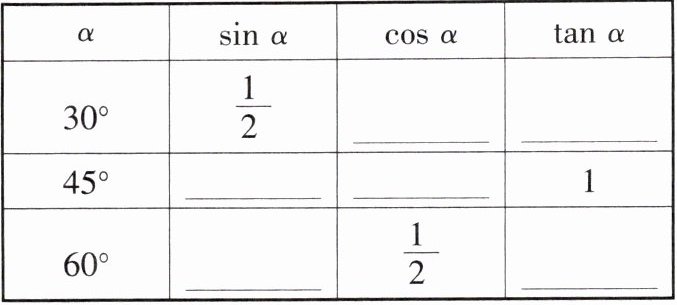
$\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{3}$
$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$
$\frac{\sqrt{3}}{2}$ $\sqrt{3}$

答案： $\frac{\sqrt{3}}{2}$ $\frac{\sqrt{3}}{3}$
$\frac{\sqrt{2}}{2}$ $\frac{\sqrt{2}}{2}$
$\frac{\sqrt{3}}{2}$ $\sqrt{3}$

小题快练
(打“√”或“×”)
1. 在直角三角形中,一个锐角的正弦就是它的对边与斜边的比。 (√)
2. 一个锐角的正弦值一定大于 $0$,余弦值一定小于 $1$。 (√)
3. $\sin^2 20 + \cos^2 30 = 1$。 (×)
4. $\cos 45° = \sin 45°$。 (√)

答案： 1.√ 2.√ 3.× 4.√

【示范题 1】在 $Rt\triangle ABC$ 中,$\angle C = 90°$,$\angle A$,$\angle B$,$\angle C$ 的对边分别为 $a$,$b$,$c$,根据下列条件,求 $\angle B$ 的三个三角函数值。
(1) $a = 9$,$b = 12$。(2) $a = \sqrt{2}$,$c = 3$。
【思路点拨】先根据勾股定理求出第三边的长,然后计算对应三角函数的值。

答案：
(1)
在$Rt\triangle ABC$中，由勾股定理得$c = \sqrt{a^{2}+b^{2}}=\sqrt{9^{2}+12^{2}} = 15$。
$\sin B=\frac{b}{c}=\frac{12}{15}=\frac{4}{5}$；
$\cos B=\frac{a}{c}=\frac{9}{15}=\frac{3}{5}$；
$\tan B=\frac{b}{a}=\frac{12}{9}=\frac{4}{3}$。
(2)
在$Rt\triangle ABC$中，由勾股定理得$b=\sqrt{c^{2}-a^{2}}=\sqrt{3^{2}-(\sqrt{2})^{2}}=\sqrt{7}$。
$\sin B=\frac{b}{c}=\frac{\sqrt{7}}{3}$；
$\cos B=\frac{a}{c}=\frac{\sqrt{2}}{3}$；
$\tan B=\frac{b}{a}=\frac{\sqrt{7}}{\sqrt{2}}=\frac{\sqrt{14}}{2}$。