《2025年配套综合练习甘肃九年级数学上册华师大版》

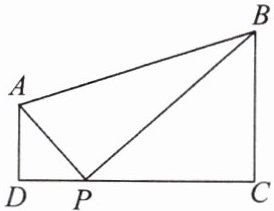
如图,AD // BC,∠D = 90°,DC = 7,AD = 2,BC = 4,若在边 DC 上有点 P 使△PAD 和△BPC 相似,则这样的点 P 的个数为 (C)

A. 1
B. 2
C. 3
D. 4
解：∵AD // BC,∠D = 90°,
∴∠C = ∠D = 90°.
又∵DC = 7,AD = 2,BC = 4,
设 PD = x,则 PC = 7 - x
由题意知,△PAD ∽ △BPC,
则 PD : BC = AD : PC,
∴$\frac{x}{4} = \frac{2}{7 - x}$,解得：PD = $\frac{7 \pm \sqrt{17}}{2}$,
∴这样的 P 点有 2 个. 选 B.
(1)错因：漏掉了PD:PC=AD:BC.即△PAD∽△PBC的情况.
(2)纠错：C 当△PAD∽△BPC时,这样的点P有2个.当△PAD∽ △PBC时PD:PC=AD:BC,即 $\frac{x}{7-x}=\frac{2}{4}$,解得PD=$\frac{7}{3}$,∴这样的P点有1个. 综上可知,点P的个数为3.

答案：
(1)漏掉了PD:PC=AD:BC.即△PAD∽△PBC的情况；
(2)C 当△PAD∽△BPC时,这样的点P有2个.当△PAD∽ △PBC时PD:PC=AD:BC,即 $\frac{x}{7-x}=\frac{2}{4}$,解得PD=$\frac{7}{3}$,
∴这样的P点有1个. 综上可知,点P的个数为3.

相似三角形的判定定理 3
1. 语言叙述：三边成比例的两个三角形相似.
2. 应用格式：如图,在△ABC 与△A'B'C'中,因为$\frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AC}{A'C'}$,所以△ABC ∽ △A'B'C'.

答案： 成比例

小题快练
(打“√”或“×”)
1. 可以利用相似三角形的判定定理 3 来判断任意两个等边三角形相似. (√)
2. 在△ABC,△DEF 中,若$\frac{AB}{DE} = \frac{DF}{AC} = \frac{BC}{EF}$,则△ABC ∽ △DEF. (×)
3. 两个直角三角形,若有两条边对应成比例,则可以判断它们相似. (×)
4. 底边和一腰对应成比例的两个等腰三角形相似. (√)

答案： 1.√ 2.× 3.× 4.√

【示范题 1】如图,四边形 ABCD,CDEF,EFGH 都是边长为 1 的正方形.
△ACF 与△GCA 相似吗？说说你的理由.

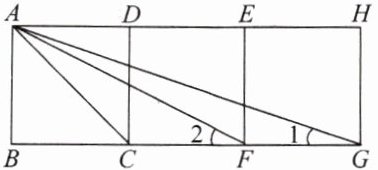
【解题探究】①如何求出△ACF 与△GCA 的各边长？
②两个三角形的对应边之间有什么关系？请写出它们之间的关系.
③结论：由①②可知△ACF 与△GCA 相似.

答案： △ACF与△GCA相似。