第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
21. (8分)已知关于$x的一元二次方程x^{2} - (2m - 1)x - 3m^{2} + m = 0$。
(1) 求证:无论$m$为何值,方程总有实数根;
(2) 若$x_{1}$,$x_{2}$是方程的两个实数根,且$\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = -\frac{5}{2}$,求$m$的值。
(1) 求证:无论$m$为何值,方程总有实数根;
(2) 若$x_{1}$,$x_{2}$是方程的两个实数根,且$\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = -\frac{5}{2}$,求$m$的值。
答案:
解析
(1)证明:
∵$\Delta=[-(2m-1)]^{2}-4×1×(-3m^{2}+m)$
$=4m^{2}-4m+1+12m^{2}-4m$
$=16m^{2}-8m+1$
$=(4m-1)^{2}\geq0$,
∴方程总有实数根.
(2)解:由题意知,$x_{1}+x_{2}=2m-1,x_{1}x_{2}=-3m^{2}+m$,
∵$\frac{x_{2}}{x_{1}}+\frac{x_{1}}{x_{2}}=\frac{x_{1}^{2}+x_{2}^{2}}{x_{1}x_{2}}=\frac{(x_{1}+x_{2})^{2}}{x_{1}x_{2}}-2=-\frac{5}{2}$,
∴$\frac{(2m-1)^{2}}{-3m^{2}+m}-2=-\frac{5}{2}$,整理得$5m^{2}-7m+2=0$,
解得m=1或$m=\frac{2}{5}$.
(1)证明:
∵$\Delta=[-(2m-1)]^{2}-4×1×(-3m^{2}+m)$
$=4m^{2}-4m+1+12m^{2}-4m$
$=16m^{2}-8m+1$
$=(4m-1)^{2}\geq0$,
∴方程总有实数根.
(2)解:由题意知,$x_{1}+x_{2}=2m-1,x_{1}x_{2}=-3m^{2}+m$,
∵$\frac{x_{2}}{x_{1}}+\frac{x_{1}}{x_{2}}=\frac{x_{1}^{2}+x_{2}^{2}}{x_{1}x_{2}}=\frac{(x_{1}+x_{2})^{2}}{x_{1}x_{2}}-2=-\frac{5}{2}$,
∴$\frac{(2m-1)^{2}}{-3m^{2}+m}-2=-\frac{5}{2}$,整理得$5m^{2}-7m+2=0$,
解得m=1或$m=\frac{2}{5}$.
22. (8分)先化简,再求值:$\frac{a^{2} - b^{2}}{a} ÷ (\frac{2ab - b^{2}}{a} - a)$,其中$a = 1 + \sqrt{2}$,$b = 1 - \sqrt{2}$。
答案:
解析原式=$\frac{(a+b)(a-b)}{a}÷(\frac{2ab-b^{2}}{a}-\frac{a^{2}}{a})=\frac{(a+b)(a-b)}{a}÷(\frac{2ab-b^{2}-a^{2}}{a})$
=$\frac{(a+b)(a-b)}{a}×\frac{a}{-(a-b)^{2}}$
=$-\frac{a+b}{a-b}$,
当$a=1+\sqrt{2},b=1-\sqrt{2}$时,
原式=$-\frac{1+\sqrt{2}+1-\sqrt{2}}{1+\sqrt{2}-1+\sqrt{2}}=-\frac{2}{2\sqrt{2}}=-\frac{\sqrt{2}}{2}$.
=$\frac{(a+b)(a-b)}{a}×\frac{a}{-(a-b)^{2}}$
=$-\frac{a+b}{a-b}$,
当$a=1+\sqrt{2},b=1-\sqrt{2}$时,
原式=$-\frac{1+\sqrt{2}+1-\sqrt{2}}{1+\sqrt{2}-1+\sqrt{2}}=-\frac{2}{2\sqrt{2}}=-\frac{\sqrt{2}}{2}$.
23. (8分)如图,在长和宽分别是$a$,$b的矩形纸片的四个角都剪去一个边长为x$的正方形。
(1) 用含$a$,$b$,$x$的代数式表示纸片剩余部分的面积。
(2) 若$a = 6$,$b = 4$,且剪去部分的面积等于剩余部分的面积时,求正方形的边长。
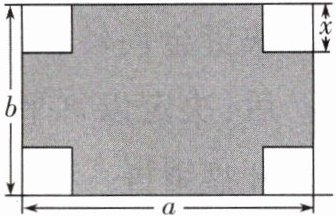
(1) 用含$a$,$b$,$x$的代数式表示纸片剩余部分的面积。
(2) 若$a = 6$,$b = 4$,且剪去部分的面积等于剩余部分的面积时,求正方形的边长。

答案:
(1)剩余部分的面积=$ab-4x^{2}$.
(2)正方形边长为$\sqrt{3}$.
(1)剩余部分的面积=$ab-4x^{2}$.
(2)正方形边长为$\sqrt{3}$.
24. (8分)同学们,在“二次根式”一章中有一个有趣的现象:$\sqrt{2\frac{2}{3}} = \sqrt{\frac{8}{3}} = \sqrt{\frac{2^{2} × 2}{3}} = 2\sqrt{\frac{2}{3}}$,根号里的因数2经过适当的演变,竟“跑”到了根号的外面,我们不妨把这种现象称为“穿墙”。具有这一性质的数还有许多,如$\sqrt{3\frac{3}{8}} = 3\sqrt{\frac{3}{8}}$、$\sqrt{4\frac{4}{15}} = 4\sqrt{\frac{4}{15}}$,等等。
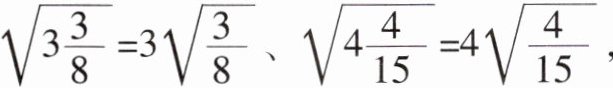
(1) 猜想:$\sqrt{6\frac{6}{35}} = $
(2) 请再写出一个具有“穿墙”性质的数:
(3) 请用只含有一个正整数$n(n \geq 2)$的等式表示上述规律:
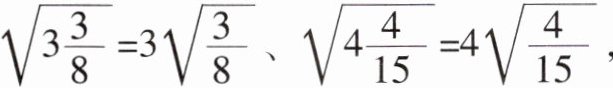
(1) 猜想:$\sqrt{6\frac{6}{35}} = $
$6\sqrt{\frac{6}{35}}$
;(2) 请再写出一个具有“穿墙”性质的数:
$\sqrt{5\frac{5}{24}}=5\sqrt{\frac{5}{24}}$
(答案不唯一,符合规律即可);(3) 请用只含有一个正整数$n(n \geq 2)$的等式表示上述规律:
$\sqrt{n\frac{n}{n^{2}-1}}=n\sqrt{\frac{n}{n^{2}-1}}$
。
答案:
解析
(1)$6\sqrt{\frac{6}{35}}$,验证如下:$\sqrt{6\frac{6}{35}}=\sqrt{\frac{216}{35}}=\sqrt{\frac{6^{2}×6}{35}}=6\sqrt{\frac{6}{35}}$.
故答案为:$6\sqrt{\frac{6}{35}}$;
(2)根据已知等式的规律可写出:$\sqrt{5\frac{5}{24}}=5\sqrt{\frac{5}{24}},...$,故答案为:$\sqrt{5\frac{5}{24}}=5\sqrt{\frac{5}{24}}$(答案不唯一,符合规律即可);
(3)第一个等式为$\sqrt{2\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,即$\sqrt{2\frac{2}{2^{2}-1}}=2\sqrt{\frac{2}{2^{2}-1}}$;
第二个等式为$\sqrt{3\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,即$\sqrt{3\frac{3}{3^{2}-1}}=3\sqrt{\frac{3}{3^{2}-1}}$;
第三个等式为$\sqrt{4\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,即$\sqrt{4\frac{4}{4^{2}-1}}=4\sqrt{\frac{4}{4^{2}-1}}$.
∴用含正整数n(n≥2)的式子表示为:$\sqrt{n\frac{n}{n^{2}-1}}=n\sqrt{\frac{n}{n^{2}-1}}$,
故答案为:$\sqrt{n\frac{n}{n^{2}-1}}=n\sqrt{\frac{n}{n^{2}-1}}$.
(1)$6\sqrt{\frac{6}{35}}$,验证如下:$\sqrt{6\frac{6}{35}}=\sqrt{\frac{216}{35}}=\sqrt{\frac{6^{2}×6}{35}}=6\sqrt{\frac{6}{35}}$.
故答案为:$6\sqrt{\frac{6}{35}}$;
(2)根据已知等式的规律可写出:$\sqrt{5\frac{5}{24}}=5\sqrt{\frac{5}{24}},...$,故答案为:$\sqrt{5\frac{5}{24}}=5\sqrt{\frac{5}{24}}$(答案不唯一,符合规律即可);
(3)第一个等式为$\sqrt{2\frac{2}{3}}=2\sqrt{\frac{2}{3}}$,即$\sqrt{2\frac{2}{2^{2}-1}}=2\sqrt{\frac{2}{2^{2}-1}}$;
第二个等式为$\sqrt{3\frac{3}{8}}=3\sqrt{\frac{3}{8}}$,即$\sqrt{3\frac{3}{3^{2}-1}}=3\sqrt{\frac{3}{3^{2}-1}}$;
第三个等式为$\sqrt{4\frac{4}{15}}=4\sqrt{\frac{4}{15}}$,即$\sqrt{4\frac{4}{4^{2}-1}}=4\sqrt{\frac{4}{4^{2}-1}}$.
∴用含正整数n(n≥2)的式子表示为:$\sqrt{n\frac{n}{n^{2}-1}}=n\sqrt{\frac{n}{n^{2}-1}}$,
故答案为:$\sqrt{n\frac{n}{n^{2}-1}}=n\sqrt{\frac{n}{n^{2}-1}}$.
查看更多完整答案,请扫码查看


