《2025年配套综合练习甘肃九年级数学上册华师大版》

1. 下列各组图形不一定相似的是 (D)
A.两个等腰直角三角形
B.各有一个角是$100°$的两个等腰三角形
C.各有一个角是$50°$的两个直角三角形
D.两个矩形

答案： D

2. 如图所示,在矩形ABCD与矩形A'B'C'D'中,AB= 1.5cm,BC= 4.5cm,A'B'= 0.8cm,B'C'= 2.4cm,这两个矩形相似。(填“相似”或“不相似”)

答案： 相似

3. 要使两个菱形相似,只需填上一个条件：有一对内角相等。

答案： 有一对内角相等

4. 小林在一边靠墙,长为6m、宽为4m的矩形的小花园周围栽种了一种蝴蝶花。如果种植的蝴蝶花一边宽AB为1m,那么当另一边宽CD为多少米时,内外边缘所围成的两个矩形相似？

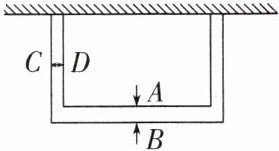
答案： 解析 设CD为xm时内外边缘所围成的两个矩形相似.由相似多边形的性质,可得$\frac{6}{4}=\frac{6+2x}{4+1}$.解得$x=\frac{3}{4}$,故当另一边宽CD为$\frac{3}{4}$m时,内外边缘所围成的两个矩形相似.

如图是某学校的矩形草坪,长40m,宽20m,沿草坪四周外围有1m宽的环形小路,小路内外边缘所形成的矩形相似吗？请说明理由。

解：因为学校的草坪是矩形,沿草坪四周的环形小路的外边缘形成的四边形也是矩形,矩形的形状都相同,因此它们相似。
(1)错因：矩形不一定相似。
(2)纠错：两个长方形的长之比=$\frac{40}{42}=\frac{20}{21}$,宽之比=$\frac{20}{22}$,$\because \frac{20}{21}\neq\frac{20}{22}$,$\therefore$它们不相似.

答案：
(1)矩形不一定相似
(2)两个长方形的长之比=$\frac{40}{42}=\frac{20}{21}$,宽之比=$\frac{20}{22}$,$\because \frac{20}{21}\neq\frac{20}{22}$,$\therefore$它们不相似.

一、相似三角形
1. 概念：
对应角相等,对应边成比例的两个三角形相似。
2. 表示法：
(1) 相似用符号“∽”表示,读作“相似于”。
(2) 若△ABC 与△DEF 相似,则可以记作：△ABC∽△DEF,读作“△ABC相似于△DEF”。
3. 相似比：
如果△ABC ∽△A'B'C',则$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$ = k,那么这个 k 就表示△ABC 与△A'B'C'的相似比。相似比就是它们的对应边的比。
4. 性质：相似三角形的对应角相等，对应边成比例。

答案： 1.相等 成比例 2.
(1)∽
(2)△ABC∽△DEF △ABC相似于△DEF 3.$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$ 对应边 4.相似三角形的对应角相等，对应边成比例