《2025年配套综合练习甘肃九年级数学上册华师大版》

一、图形运动问题
1. 点 $ A $ 在直线 $ l $ 上运动,速度为 $ 1cm/s $,则 $ t s $ 后点 $ A $ 移动的距离为tcm。
2. 点 $ B $ 在长为5cm的线段 $ a $ 上运动,速度为 $ 1cm/s $,则点 $ B $ 运动时间 $ t $ 的范围是$0≤t≤5$s。

答案： 1.t 2.$0≤t≤5$

二、利润问题中的数量关系
1. 利润 = 售价 - 进价。
2. 利润率 = 利润 ÷ 进价。
3. 总利润 = 每件利润 × 销售量 = 总收入 - 总支出。

答案： 1.进价 2.进价 3.销售量 总支出

三、体育比赛场次类问题的数量关系
1. $ m $ 支球队,单循环比赛(每两支球队之间都赛一场),共需进行$m(m-1)÷2$场比赛。
2. $ m $ 支球队,双循环比赛(每两支球队之间都赛两场),共需进行$m(m-1)$场比赛。

答案： 1.$m(m-1)÷2$ 2.$m(m-1)$

小题快练
(打“√”或“×”)
1. 打折售价的算法：售价 = 定价 × 折扣率。(√)
2. 翻一番为原来的2倍；翻两番为原来的4倍。(√)
3. 某一商品进货价便宜8%,而售价不变,那么它的利润为原利润再增加8%。(×)
4. 三个连续整数的平方和为29,则这三个连续整数为2,3,4。(×)

答案： 1.√ 2.√ 3.× 4.×

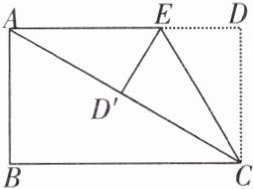
【示范题1】如图,将长方形纸片 $ ABCD $ 折叠,使边 $ DC $ 落在对角线 $ AC $ 上,折痕为 $ CE $,且 $ D $ 点落在 $ D' $ 处,若 $ AB = 3 $,$ AD = 4 $,则 $ ED $ 的长为(A)

A.$ \frac{3}{2} $
B.3
C.1
D.$ \frac{4}{3} $

答案： A【解答】
∵ 在矩形 $ ABCD $ 中,$ CD = AB = 3 $,$ ∠D = 90° $,$ AD = 4 $,

∴ 在 $ Rt△ACD $ 中,由勾股定理知 $ AC = \sqrt{AD^2 + CD^2} = 5 $,由折叠可知 $ CD' = CD = 3 $,$ ED' = ED $,$ AD' = 5 - 3 = 2 $,$ ∠AD'E = 90° $,设 $ ED = x $,则在 $ Rt△AD'E $ 中,$ ED' = x $,$ AE = 4 - x $,由勾股定理可得方程 $ (4 - x)^2 = 2^2 + x^2 $,解得 $ x = \frac{3}{2} $。故选A。
【思路点拨】由 $ AB = 3 $,$ AD = 4 $ → 求 $ AC $ 的长 → 设 $ ED = x $ → 表示 $ AE $ 和 $ ED' $ → 根据 $ Rt△AD'E $ 的三边长列方程 → 得 $ ED $。

【示范题2】小丽为校合唱队购买某种服装时,商店经理给出了如下优惠条件,如果一次性购买不超过10件,单价为80元；如果一次性购买多于10件,那么每增加1件,购买的所有服装的单价降低2元,但单价不得低于50元,按此优惠条件,小丽一次性购买这种服装付了1200元,请问她购买了多少件这种服装？

答案： 设她购买了 $x$ 件这种服装。
根据优惠条件，单价为 $80 - 2(x - 10)$ 元（当 $x ＞ 10$ 时）。
因此，总价为 $x × [80 - 2(x - 10)] = 1200$。
展开方程得：
$x(80 - 2x + 20) = 1200$，
$x(100 - 2x) = 1200$，
$100x - 2x^2 = 1200$，
$2x^2 - 100x + 1200 = 0$，
$x^2 - 50x + 600 = 0$。
解这个一元二次方程，得到：
$(x - 20)(x - 30) = 0$，
$x_1 = 20, \quad x_2 = 30$。
检验：
当 $x = 30$ 时，单价为 $80 - 2(30 - 10) = 40$ 元，但单价不得低于 50 元，所以 $x = 30$ 不合题意，舍去。
当 $x = 20$ 时，单价为 $80 - 2(20 - 10) = 60$ 元，符合题意。
答：她购买了 20 件这种服装。