第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
【示范题2】如图所示的两个矩形是否相似?并简单说明理由。
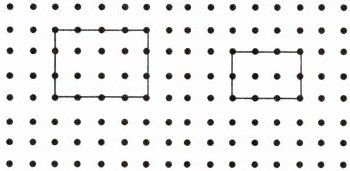

答案:
两个矩形不相似。
理由:
判断角:
$\because$矩形的四个角都是直角,
$\therefore $两个矩形的对应角相等。
判断边:
在图中可测量出:
第一个矩形长为$3$个单位长度,宽为$2$个单位长度;
第二个矩形长为$4$个单位长度,宽为$3$个单位长度。
两个矩形宽之比为$\frac{2}{3}$,长之比为$\frac{3}{4}$。
$\because \frac{2}{3} \neq \frac{3}{4}$,
$\therefore $两个矩形的对应边不成比例。
结论:
两个矩形不相似。
理由:
判断角:
$\because$矩形的四个角都是直角,
$\therefore $两个矩形的对应角相等。
判断边:
在图中可测量出:
第一个矩形长为$3$个单位长度,宽为$2$个单位长度;
第二个矩形长为$4$个单位长度,宽为$3$个单位长度。
两个矩形宽之比为$\frac{2}{3}$,长之比为$\frac{3}{4}$。
$\because \frac{2}{3} \neq \frac{3}{4}$,
$\therefore $两个矩形的对应边不成比例。
结论:
两个矩形不相似。
1. 如图所示的两个五边形相似,∠α的度数是 (
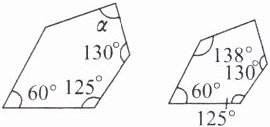
A.$75°$
B.$60°$
C.$87°$
D.$120°$
C
)
A.$75°$
B.$60°$
C.$87°$
D.$120°$
答案:
C
2. 如图,把一个长方形分成两个全等的小长方形,若使每一个小长方形与原长方形相似,则原长方形长和宽之比为 (

A.$2:1$
B.$3:1$
C.$\sqrt{2}:1$
D.$\sqrt{3}:1$
C
)
A.$2:1$
B.$3:1$
C.$\sqrt{2}:1$
D.$\sqrt{3}:1$
答案:
C
3. 如果两个相似多边形的最长边分别为35cm和14cm,那么相应的最短边分别为5cm和
2
cm。
答案:
2
4. 已知四边形ABCD与四边形$A_1B_1C_1D_1$相似,且AB:BC:CD:DA= 20:15:9:8,四边形$A_1B_1C_1D_1$的周长为26,求四边形$A_1B_1C_1D_1$的各边长。
答案:
解析 四边形ABCD与四边形A₁B₁C₁D₁相似,对应边成比例,AB:BC:CD:DA=20:15:9:8,则不妨设A₁B₁:B₁C₁:C₁D₁:D₁A₁=20:15:9:8,设A₁B₁=20x.则B₁C₁=15x,C₁D₁=9x,D₁A₁=8x,根据四边形A₁B₁C₁D₁的周长为26得到:20x+15x+9x+8x=26,解得x=0.5,
∴四边形A₁B₁C₁D₁的各边长 参考答案 分别为10,7.5,4.5,4.
∴四边形A₁B₁C₁D₁的各边长 参考答案 分别为10,7.5,4.5,4.
查看更多完整答案,请扫码查看


