《2025年配套综合练习甘肃九年级数学上册华师大版》

1. 下列运算正确的是 (D)

A. x - 2 x = x
B. ( x y ) ^ { 2 } = x y ^ { 2 }
$C. ( - \sqrt{2} ) ^ { 2 } = 4 $
$D. \sqrt{2} × \sqrt{3} = \sqrt{6} $

答案： D

2. 等式$ \sqrt{x + 1} \cdot \sqrt{x - 1} = \sqrt{x ^ { 2 } - 1} $成立的条件是 (A)
$A. x \geq 1 B. x \geq - 1 $
$C. - 1 \leq x \leq 1 $
$D. 全体实数$

答案： A

3. 把 $$ - 3 \sqrt{\frac{a}{3}} ( a \geq 0 ) $$ 根号外的因式移到根号内所得结果为 (D)
$A. - \sqrt{a} $
$B. \sqrt{- a} $
$C. - 3 \sqrt{a} $
$D. - \sqrt{3 a} $

答案： D

4. 计算 $$ \sqrt{8} × \sqrt{\frac{1}{2}} + ( \sqrt{2} ) ^ { 0 } $$ 的结果为 (C)
$A. 2 + \sqrt{2} $
$B. \sqrt{2} + 1 $
C.3
D.5

答案： C

5. 计算 $$ x \cdot \sqrt{2 x} \cdot 5 \sqrt{6 x y} ( x \geq 0 , y \geq 0 ) $$ 等于 (A)
$A. 10 x ^ { 2 } \sqrt{3 y} $
B. 60 x ^ { 3 } y
$C. 5 x ^ { 2 } \sqrt{12 y} $
$D. 5 x \sqrt{12 y} $

答案： A

6. $\sqrt{\frac{1}{2}} × \sqrt{162} = $9.

答案： 9

7. 计算：$ \sqrt{a} \cdot \sqrt{a b} ( a \geq 0 , b \geq 0 ) = $$a\sqrt{b}$.

答案： $a\sqrt{b}$

8. $$ \sqrt{\frac{b}{a}} \cdot \sqrt{\frac{a}{c}} \cdot \sqrt{\frac{c}{b}} ( a , b , c $$ 同时大于 0 或 $$ a , b , c $$ 同时小于 0 ) 的值为 1.

答案： 1

9. 先化简,再求值： ( x + 1 ) ^ { 2 } - x ( x + 2 y ) - 2 x , 其中$ x = \sqrt{3} + 1 , y = \sqrt{3} - 1 . $

答案： 解析$(x+1)^{2}-x(x+2y)-2x$$=x^{2}+2x+1-x^{2}-2xy-2x=1-2xy$.当$x=\sqrt{3}+1$,$y=\sqrt{3}-1$时,原式$=1-2(\sqrt{3}+1)(\sqrt{3}-1)$$=1-2[(\sqrt{3})^{2}-1^{2}]$$=1-2×(3-1)=1-4=-3$

计算：$ \sqrt{2 a b} × \sqrt{\frac{b}{8 a}} ( a b \geq 0 , a \neq 0 ) $. $解：$$ \sqrt{2 a b} × \sqrt{\frac{b}{8 a}} = \sqrt{2 a b \cdot \frac{b}{8 a}} = \sqrt{\frac{b ^ { 2 }}{4}} = \frac{b}{2} $

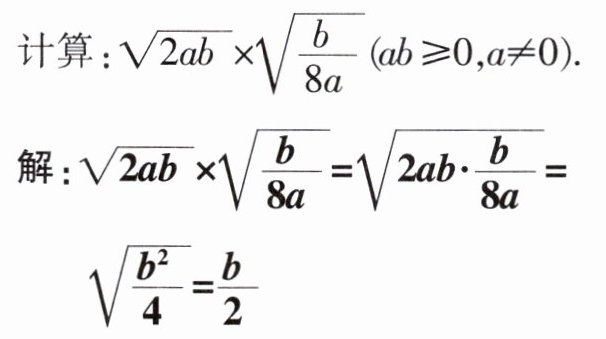
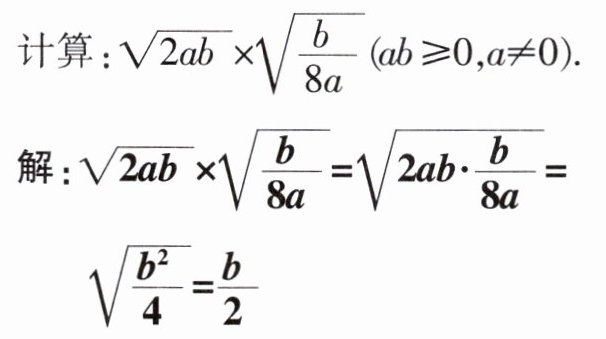
(1) 错因：由题意知a,b同号,但b不一定为正 数学配套综合练习 九.
(2) 纠错：当$b\geqslant 0$时,原式$=\frac{b}{2}$;当$b＜0$时,原式$=-\frac{b}{2}$.

答案：
(1)由题意知a,b同号,但b不一定为正 数学配套综合练习 九
(2)当$b\geqslant 0$时,原式$=\frac{b}{2}$;当$b＜0$时,原式$=-\frac{b}{2}$