第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
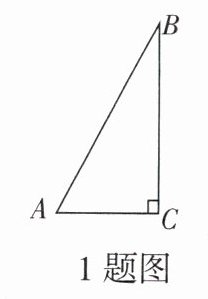
1. 如图,若∠A= 60°,AC= 20m,则BC大约是(结果精确到0.1m)(
A.34.64m
B.34.6m
C.28.3m
D.17.3m
B
)
A.34.64m
B.34.6m
C.28.3m
D.17.3m
答案:
B
2. 如图,在△ABC中,∠A= 45°,∠B= 30°,CD⊥AB,垂足为D,CD= 1,则AB的长为
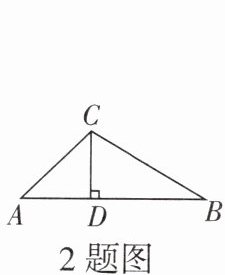
√3 + 1
。
答案:
√3 + 1
3. 如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为
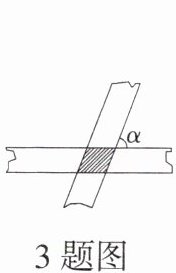
1/sinα
。
答案:
1/sinα
1. 如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12km到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是
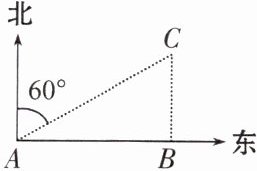
4√3 km
。
答案:
4√3 km
2. 如图,已知灯塔A的周围7km的范围内有暗礁,一艘渔轮在B处测得灯塔A在北偏东60°的方向,向正东航行8km到C处后,又测得该灯塔在北偏东30°方向,渔轮不改变航向,继续向东航行,有没有触礁危险?请通过计算说明理由。(参考数据$\sqrt{3}$≈1.732)
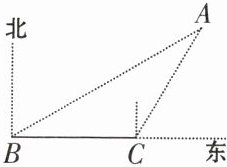

答案:
有触礁危险,理由略
在一个含30°角的直角三角形中,一条边的长为1,另一条边的长为2.那么这个三角形的面积有
解:如图,有两种结果,
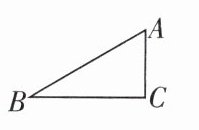
第一种:∠B= 30°,∠ACB= 90°,
AC= 1,AB= 2,∴BC= $\sqrt{AB^{2}-AC^{2}}$= $\sqrt{3}$,
∴S△ABC= $\frac{1}{2}$AC×BC= $\frac{\sqrt{3}}{2}$。
第二种:∠B= 30°,AC= 1,BC= 2,
∴S△ABC= $\frac{1}{2}$AC×BC= 1。
(1)错因:
(2)纠错:
1
种结果。解:如图,有两种结果,

第一种:∠B= 30°,∠ACB= 90°,
AC= 1,AB= 2,∴BC= $\sqrt{AB^{2}-AC^{2}}$= $\sqrt{3}$,
∴S△ABC= $\frac{1}{2}$AC×BC= $\frac{\sqrt{3}}{2}$。
第二种:∠B= 30°,AC= 1,BC= 2,
∴S△ABC= $\frac{1}{2}$AC×BC= 1。
(1)错因:
长为2的边只能为斜边,不可能为直角边
。(2)纠错:
只有一种情况,在Rt△ABC中,30°角对的直角边为1,斜边为2,则S△ABC = 1/2×1×√(2² - 1²)=√3/2
。
答案:
(1)长为2的边只能为斜边,不可能为直角边.
(2)只有一种情况,在Rt△ABC中,30°角对的直角边为1,斜边为2,则S△ABC = 1/2×1×√(2² - 1²)=√3/2
答案1.
(2)只有一种情况,在Rt△ABC中,30°角对的直角边为1,斜边为2,则S△ABC = 1/2×1×√(2² - 1²)=√3/2
答案1.
查看更多完整答案,请扫码查看


