《2025年配套综合练习甘肃九年级数学上册华师大版》

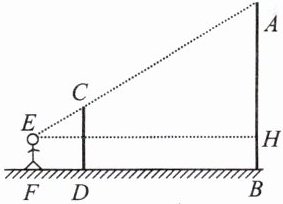
2. 为测量操场上悬挂国旗的旗杆高度,设计的测量方案如图所示：标杆高度 $ CD = 3m $,标杆与旗杆的水平距离 $ BD = 15m $,人的眼睛与地面的高度 $ EF = 1.6m $,人与标杆 $ CD $ 的水平距离 $ DF = 2m $,$ E $,$ C $,$ A $ 三点共线,则旗杆 $ AB $ 的高度为13.5 $ m $。

答案： 13.5

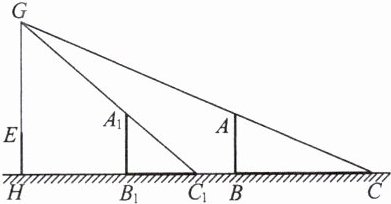
3. 小刚、小雯想利用灯光下自己的影子长度来测量一路灯的高度。如图所示,在同一时间,身高为 $ 1.6m $ 的小刚($ AB $)的影子($ BC $)长是 $ 3m $,而小雯($ EH $)刚好在路灯灯泡的正下方 $ H $ 点,并测得 $ HB = 6m $。
(1) 求路灯灯泡的垂直高度 $ GH $。
(2) 如果小刚沿线段 $ BH $ 向小雯($ EH $)走去,当小刚走到 $ BH $ 中点 $ B_1 $ 处时(如图所示),求其影子 $ B_1C_1 $ 的长。

答案：
(1)∠ABC=∠GHC=90°,∠C=∠C,
∴△ABC∽△GHC,
∴$\frac{AB}{GH}=\frac{BC}{HC}$,即$\frac{1.6}{GH}=\frac{3}{6+3}$,
∴GH=4.8(m).
(2)由题意得:∠$A_1B_1C_1$=∠GHC₁=90°,∠$A_1C_1B_1$=∠GC₁H,
∴△$A_1B_1C_1$∽△GHC₁,
∴$\frac{A_1B_1}{GH}=\frac{B_1C_1}{HC_1}$.设$B_1C_1$长为xm,则$\frac{1.6}{4.8}=\frac{x}{x+3}$,解得$x=\frac{3}{2}$,即$B_1C_1=\frac{3}{2}$m.

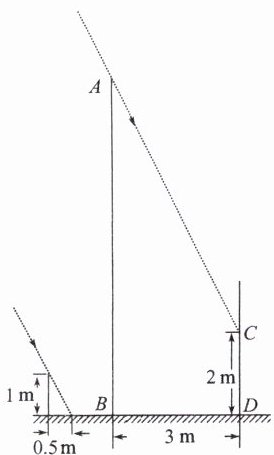
如图,一电线杆 $ AB $ 的影子分别落在了地上和墙上,某一时刻,小明竖起 $ 1m $ 高的直杆,量得其影长为 $ 0.5m $,此时,他又量得电线杆 $ AB $ 落在地上的影子 $ BD $ 长 $ 3m $,落在墙上的影子 $ CD $ 的高为 $ 2m $。小明用这些数据很快算出了电线杆 $ AB $ 的高。请你计算,电线杆 $ AB $ 的高为(D)

A. $ 5m $
B. $ 6m $
C. $ 7m $
D. $ 8m $
解：$ \because $ 直杆影长与电线杆影长成正比例。
$ \therefore AB:BD = 1:0.5 $ ①
$ \because BD = 3m $。$ \therefore AB = 6m $ ②
选 B。
(1) 找错：从第①步开始出现错误。
(2) 纠错：延长AC交直线BD于E,则$\frac{CD}{DE}=\frac{1}{0.5}$,∴DE=1m.∵△ABE∽△CDE,∴$\frac{AB}{CD}=\frac{BE}{DE}$,∴$\frac{AB}{2}=\frac{3+1}{1}$,∴AB=8m.

答案：
(1)①
(2)延长AC交直线BD于E,则$\frac{CD}{DE}=\frac{1}{0.5}$,
∴DE=1m.
∵△ABE∽△CDE,
∴$\frac{AB}{CD}=\frac{BE}{DE}$,
∴$\frac{AB}{2}=\frac{3+1}{1}$,
∴AB=8m.

一、三角形的中位线
1. 概念：连结三角形两边中点的线段叫做三角形的中位线。
2. 定理：三角形的中位线平行于第三边,并且等于第三边的一半。

答案： 1. 中点 2. 平行于 一半