《2025年配套综合练习甘肃九年级数学上册华师大版》

1. 同一时刻,有一身高 $ 2.26m $ 的运动员阳光下影长为 $ 1.13m $；林浩在阳光下的影长为 $ 0.64m $,则林浩的身高为1.28m。

答案： 1.28m

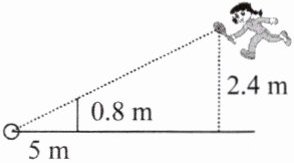
2. 如图,小芳在打网球时,为使球恰好能过网(网高为 $ 0.8m $)且落在对方区域离网 $ 5m $ 的位置处,已知她击球的高度是 $ 2.4m $,则她应站在离网10m 处。

答案： 10

1. 小明在一次夏令营活动中进行打靶训练,在用枪瞄准目标点 $ B $ 时,要使眼睛 $ O $、准星 $ A $、目标 $ B $ 在同一条直线上,如图所示,在射击时,小明有轻微的抖动,致使准星 $ A $ 偏离到 $ A' $,若 $ OA = 0.2m $,$ OB = 40m $,$ AA' = 0.0015m $,则小明射击到的点 $ B' $ 偏离目标点 $ B $ 的长度 $ BB' $ 为(B)

A.$ 3m $
B.$ 0.3m $
C.$ 0.03m $
D.$ 0.2m $

答案： B

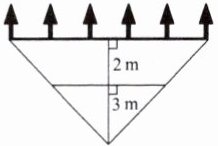
2. 如图所示,某校宣传栏后面 $ 2m $ 处种了一排树,每隔 $ 2m $ 一棵,共种了 $ 6 $ 棵,小勇站在距宣传栏中间位置的垂直距离 $ 3m $ 处,正好看到两端的树干,其余的 $ 4 $ 棵均被挡住,那么宣传栏的长为6m。(不计宣传栏的厚度)

答案： 6

如图,小东用长为 $ 3.2m $ 的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点。此时,竹竿与这一点相距 $ 8m $,与旗杆相距 $ 22m $,则旗杆 $ BC $ 的高为______。

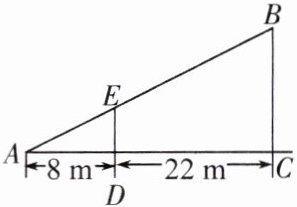
解：$\because ED \perp AD$,$BC \perp AC$,
$\therefore ED // BC$,$\therefore \triangle AED \sim \triangle ABC$,
$\therefore \frac{AD}{DC} = \frac{DE}{BC}$。
又 $\because AD = 8m$,$DC = 22m$,$DE = 3.2m$,
$\therefore BC = 8.8m$。
(1)错因：对应边寻找错误。
(2)纠错：∵$\frac{AD}{AC}=\frac{DE}{BC}$，$\frac{8}{8+22}=\frac{3.2}{BC}$，∴$BC=12m$。

答案：
(1)对应边寻找错误
(2)
∵$\frac{AD}{AC}=\frac{DE}{BC}$，$\frac{8}{8+22}=\frac{3.2}{BC}$，
∴$BC=12m$.