《2025年新课程课堂同步练习册九年级数学上册华师大版》

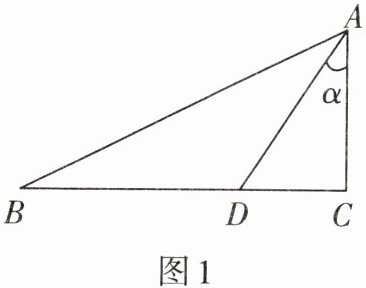
2. 如图1,已知在$\text{Rt}\triangle ABC$中,$\angle C= 90^\circ$,$D是BC$上一点,$AC= 2$,$CD= 1$,$\angle CAD= \alpha$.
(1)试写出$\alpha$的三个三角函数值;
(2)若$\angle B= \angle CAD= \alpha$,求$BD$的长.

答案： 【解析】：
本题主要考查了锐角三角函数的定义及运用。
（1）在直角三角形$ACD$中，已知$AC = 2$，$CD = 1$，根据勾股定理，可以求出$AD$的长度。
再根据三角函数的定义，可以求出$\angle CAD = \alpha$的三个三角函数值。
（2）在直角三角形$ABC$中，已知$\angle B = \alpha$，$AC = 2$，
可以通过三角函数求出$BC$的长度，再用$BC$的长度减去$CD$的长度，即可得到$BD$的长度。
【答案】：
(1)在$\text{Rt}\triangle ACD$中，$AC = 2$，$CD = 1$，
根据勾股定理，有
$AD = \sqrt{AC^{2} + CD^{2}} = \sqrt{2^{2} + 1^{2}} = \sqrt{5}$，
因此，
$\sin\alpha = \frac{CD}{AD} = \frac{1}{\sqrt{5}} = \frac{\sqrt{5}}{5}$，
$\cos\alpha = \frac{AC}{AD} = \frac{2}{\sqrt{5}} = \frac{2\sqrt{5}}{5}$，
$\tan\alpha = \frac{CD}{AC} = \frac{1}{2}$；
(2)在$\text{Rt}\triangle ABC$中，$\angle B = \alpha$，$AC = 2$，
故
$BC = \frac{AC}{\tan\alpha} = \frac{2}{\frac{1}{2}} = 4$，
因此，
$BD = BC - CD = 4 - 1 = 3$。

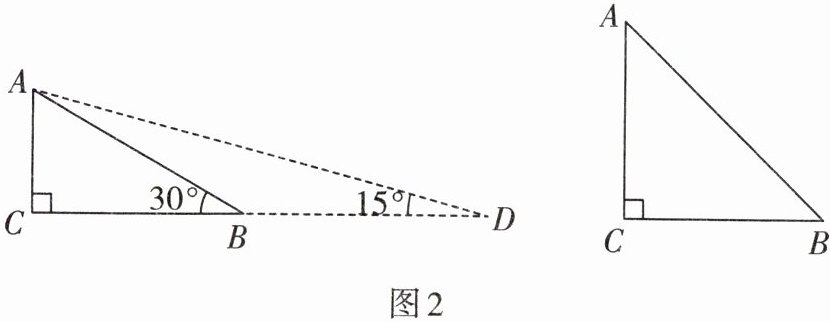
3. 为计算$\tan15^\circ$的三角函数值,我们可以构建$\text{Rt}\triangle ACB$,如图2,使得$\angle C= 90^\circ$,$\angle ABC= 30^\circ$,延长$CB到点D$,使$BD= AB$,连结$AD$,可得到$\angle D= 15^\circ$,所以$\tan15^\circ=\frac{AC}{CD}= \frac{1}{2+\sqrt{3}}= \frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}= 2-\sqrt{3}$.类比这种方法,请你计算$\tan22.5^\circ$的值.

答案： 解：构建Rt△ACB，使∠C=90°，∠ABC=45°，延长CB到点D，使BD=AB，连结AD。
设AC=1，在Rt△ACB中，∠ABC=45°，则BC=AC=1，AB=√(AC²+BC²)=√2。
∵BD=AB，
∴BD=√2，∠BAD=∠D。
∵∠ABC=∠BAD+∠D=45°，
∴∠D=22.5°。
CD=BC+BD=1+√2。
tan22.5°=AC/CD=1/(1+√2)=(√2-1)/[(1+√2)(√2-1)]=√2-1。
答：tan22.5°的值为√2-1。