《2025年新课程课堂同步练习册九年级数学上册华师大版》

2. 一商店销售某种商品,平均每天可售出20件,每件盈利40元. 为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价3元,则平均每天销售数量为26件;
(2)当每件商品降价多少元时,该商店每天销售利润为1200元?解：设每件商品降价$x$元。
根据题意，得$(40 - x)(20 + 2x) = 1200$
展开并整理，得$x^2 - 30x + 200 = 0$
解得$x_1 = 10$，$x_2 = 20$
因为每件盈利不少于25元，所以$40 - x \geq 25$，即$x \leq 15$
$x_2 = 20$不合题意，舍去。
答：当每件商品降价10元时，该商店每天销售利润为1200元。

答案：
(1)26
(2)解：设每件商品降价$x$元。
根据题意，得$(40 - x)(20 + 2x) = 1200$
展开并整理，得$x^2 - 30x + 200 = 0$
解得$x_1 = 10$，$x_2 = 20$
因为每件盈利不少于25元，所以$40 - x \geq 25$，即$x \leq 15$
$x_2 = 20$不合题意，舍去。
答：当每件商品降价10元时，该商店每天销售利润为1200元。

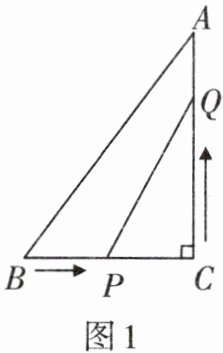
3. 如图1,在△ABC中,∠C= 90°,BC= 5 cm,AC= 7 cm. 两个动点P,Q分别从B,C两点同时出发,其中点P以1cm/s的速度沿着线段BC向点C运动,点Q以2 cm/s的速度沿着线段CA向点A运动.
(1)P,Q两点在运动过程中,经过几秒后,△PCQ的面积等于$4 cm^2? $经过几秒后PQ的长度等于5 cm?
(2)P,Q两点在运动过程中,四边形ABPQ的面积能否等于$11 cm^2? $试说明理由.

答案： 解：
(1)设经过t秒后，△PCQ的面积等于4cm²。
由题意得：PC=BC-BP=5-t，CQ=2t。
∵∠C=90°，
∴S△PCQ=1/2·PC·CQ=1/2(5-t)·2t=4，
整理得：t²-5t+4=0，
解得：t₁=1，t₂=4。
∵点P运动到点C需5秒，点Q运动到点A需7÷2=3.5秒，
∴t=4不合题意，舍去。
∴t=1。
设经过t秒后PQ的长度等于5cm。
由题意得：PC=5-t，CQ=2t。
∵∠C=90°，
∴PQ²=PC²+CQ²，
即(5-t)²+(2t)²=5²，
整理得：5t²-10t=0，
解得：t₁=0（不合题意，舍去），t₂=2。
∵t=2≤3.5，
∴t=2。
(2)四边形ABPQ的面积不能等于11cm²。理由如下：
S△ABC=1/2·AC·BC=1/2×7×5=17.5cm²。
若四边形ABPQ的面积等于11cm²，则S△PCQ=S△ABC-S四边形ABPQ=17.5-11=6.5cm²。
由题意得：1/2(5-t)·2t=6.5，
整理得：t²-5t+6.5=0，
∵Δ=(-5)²-4×1×6.5=25-26=-1＜0，
∴方程无实数根，
∴四边形ABPQ的面积不能等于11cm²。
答：
(1)经过1秒后，△PCQ的面积等于4cm²；经过2秒后PQ的长度等于5cm。
(2)四边形ABPQ的面积不能等于11cm²。