《2025年新课程课堂同步练习册九年级数学上册华师大版》

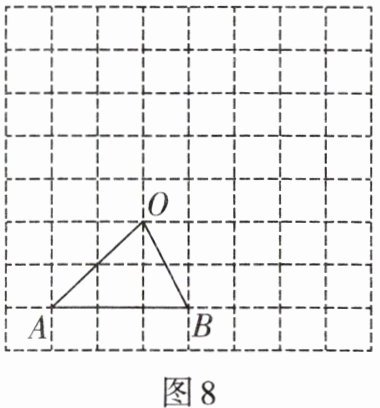
2. 如图8,在8×8的网格图中,每个小正方形的顶点叫做格点,△OAB的顶点都在格点上,请在

网

格

图

中

画

出

△OAB的一个位似图形,使两个图形以O为位似中心,且所画图形与△OAB的位似比为2:1.

答案： 解：
1. 连接OA并延长，使延长部分长度等于OA，得到点A'；
2. 连接OB并延长，使延长部分长度等于OB，得到点B'；
3. 连接A'B'，则△OA'B'即为所求位似图形（位似比2:1，与△OAB在O同侧）。
（注：若延长方向相反，在O异侧可得到另一个位似图形△OA''B''，画法类似，延长OA、OB至反向两倍长度即可。）
（此处需在网格图中按上述步骤画出图形，文字描述仅为作图依据。）

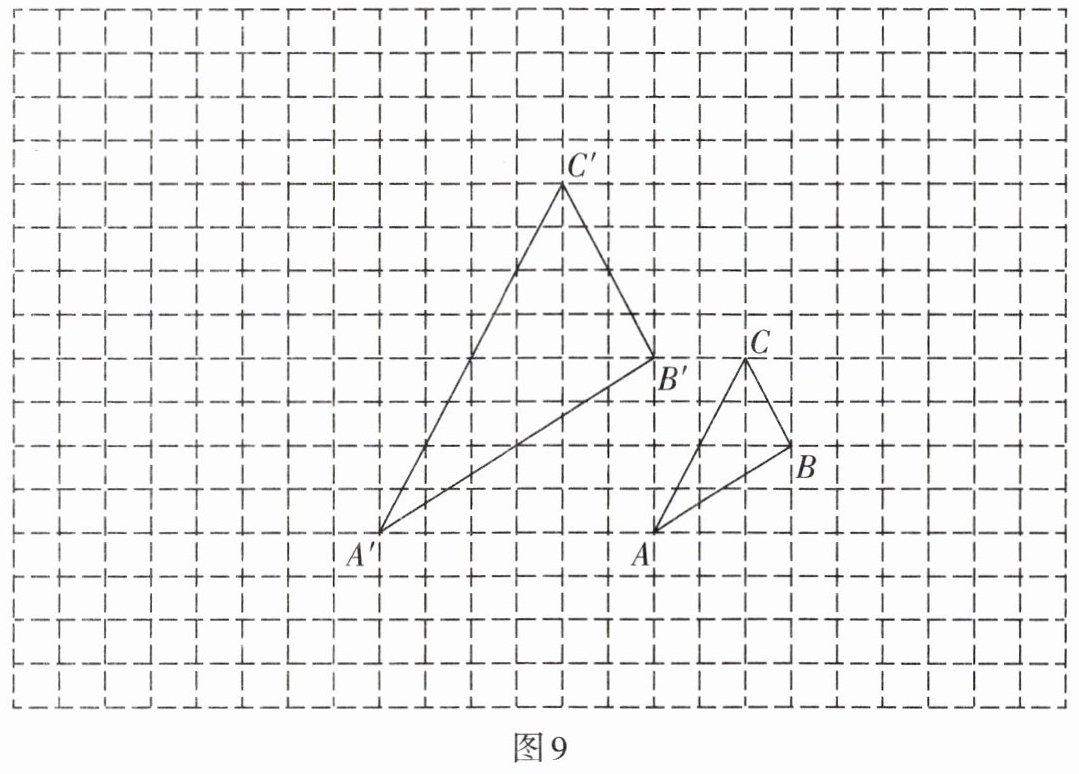
3. 如图9,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是关于点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的位似比;
(3)以点O为位似中心,再画一个△A''B''C'',使它与△ABC的位似比等于3.

答案：
(1) 位似中心点O如图所示（通过连接对应点A与A'、B与B'，其延长线交点即为O）。
(2) 解：由图可知，$AC=√[(2)^2+(2)^2]=2√2，$$A'C'=√[(4)^2+(4)^2]=4√2，$位似比为AC:A'C'=2√2:4√2=1:2。
(3) 如图所示（以O为位似中心，延长OA到A''使OA''=3OA，同法得到B''、C''，连接A''B''、B''C''、C''A''）。

1. 课间操时,小华、小军、小刚的位置如图1,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(D)
A.(5,4)
B.(4,5)
C.(3,4)
D.(4,3)

答案： 解：以小华为原点(0,0)建立平面直角坐标系，小军位置为(2,1)，可知图中每个小方格边长为1个单位长度，水平向右为x轴正方向，竖直向上为y轴正方向。
小刚在小华右边4个单位，上方3个单位，故小刚位置为(4,3)。
答案：D