《2025年新课程课堂同步练习册九年级数学上册华师大版》

3. 已知$\triangle ABC$,在如图10的正方形网格纸中:
(1)画一个$\triangle DEF$,使$\triangle ABC和\triangle DEF的相似比为1$;
(2)画一个$\triangle GHI$,使$\triangle ABC和\triangle GHI的相似比为\frac{1}{2}$.

答案：
(1) 解：在网格中画一个与△ABC全等的三角形，如以点(4,0)为D，(5,1)为E，(7,1)为F，连接D、E、F，得到△DEF，此时△ABC与△DEF相似比为1。（画图略，具体位置不唯一，只要全等即可）
(2) 解：先计算△ABC各边长度（设网格边长为1），AB=√[(1-0)²+(1-2)²]=√2，BC=2，AC=√[(2-0)²+(1-2)²]=√5。相似比为1/2，则△GHI各边为AB'=2√2，B'C'=4，A'C'=2√5。在网格中取点(0,3)为G，(2,5)为H，(6,5)为I，连接G、H、I，得到△GHI。（画图略，具体位置不唯一，满足边长比例即可）

4. 如图11,在矩形$ABCD$中,点$E$,$F分别在边AD$,$DC$上,$\triangle ABE \backsim \triangle DEF$,且$\angle 1= \angle 2$,$AB= 6$,$AE= 9$,$DE= 2$,求$EF$的长.

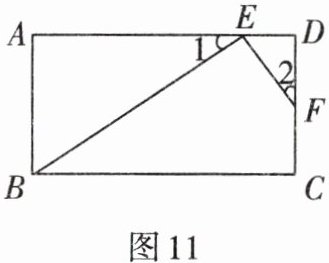
答案： 解：
∵ 四边形 $ABCD$ 是矩形，
∴ $\angle A = \angle D = 90^\circ$。
∵ $\triangle ABE \backsim \triangle DEF$，
∴ $\frac{AB}{DE} = \frac{AE}{DF}$。
∵ $AB = 6$，$AE = 9$，$DE = 2$，
∴ $\frac{6}{2} = \frac{9}{DF}$，解得 $DF = 3$。
在 $\text{Rt}\triangle DEF$ 中，$\angle D = 90^\circ$，
∴ $EF = \sqrt{DE^2 + DF^2} = \sqrt{2^2 + 3^2} = \sqrt{13}$。
答：$EF$ 的长为 $\sqrt{13}$。

1. 在△ABC与△A'B'C'中,$∠B= ∠B'= 90^\circ,$$∠A= 30^\circ,$则以下条件不能说明△ABC与△A'B'C'相似的是$( )A. ∠A'= 30^\circB. ∠C'= 60^\circC. ∠C= 60^\circD. ∠C'= 2∠A'$C

答案： 解：在△ABC中，∠B=90°，∠A=30°，则∠C=60°。
A. ∠A'=30°，∠B'=90°，则∠C'=60°，∠A=∠A'，∠B=∠B'，∠C=∠C'，△ABC∽△A'B'C'。
B. ∠C'=60°，∠B'=90°，则∠A'=30°，∠A=∠A'，∠B=∠B'，∠C=∠C'，△ABC∽△A'B'C'。
C. ∠C=60°是△ABC自身内角，未提及△A'B'C'角度关系，不能说明相似。
D. ∠C'=2∠A'，∠B'=90°，则∠A'+∠C'=90°，即∠A'+2∠A'=90°，∠A'=30°，∠C'=60°，∠A=∠A'，∠B=∠B'，∠C=∠C'，△ABC∽△A'B'C'。
答案：C

2. 如图1,在△ABC中,$∠BAC= 90^\circ,$AD⊥BC于点D,图中相似三角形共有(B)
A.4对
B.3对
C.2对
D.1对

答案： 解：
∵∠BAC=90°，AD⊥BC，
∴∠ADB=∠ADC=∠BAC=90°．
在△ABC和△DBA中，
∠B=∠B，∠BAC=∠ADB，
∴△ABC∽△DBA（AA）．
在△ABC和△DAC中，
∠C=∠C，∠BAC=∠ADC，
∴△ABC∽△DAC（AA）．
∵△ABC∽△DBA，△ABC∽△DAC，
∴△DBA∽△DAC（相似三角形的传递性）．
综上，图中相似三角形共有3对．
答案：B

3. 如图2,在△ABC纸片中,$∠A= 76^\circ,$$∠B= 34^\circ. $将△ABC纸片沿某处剪开,下列四种方式中剪下的阴影三角形与原三角形相似的是(A)
A.①②
B.②④
C.①③
D.③④

答案： A