《2025年新课程课堂同步练习册九年级数学上册华师大版》

1. 如图9,在$\triangle ABC$中,$MD// AB$,$MN// AE$.求证:$\frac{CD}{CB}= \frac{CN}{CE}$.

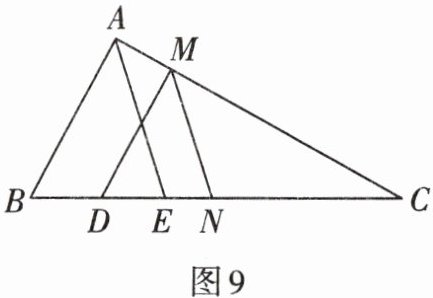
答案： 【解析】：
本题可根据平行线分线段成比例定理来证明$\frac{CD}{CB}= \frac{CN}{CE}$。
已知$MD// AB$，根据平行线分线段成比例定理，可得$\frac{CD}{CB}=\frac{CM}{CA}$；
又因为$MN// AE$，同样根据平行线分线段成比例定理，可得$\frac{CN}{CE}=\frac{CM}{CA}$。
所以由上述两个等式可推出$\frac{CD}{CB}= \frac{CN}{CE}$。
【答案】：
证明：
∵$MD// AB$，
∴$\frac{CD}{CB}=\frac{CM}{CA}$（平行线分线段成比例定理）。
∵$MN// AE$，
∴$\frac{CN}{CE}=\frac{CM}{CA}$（平行线分线段成比例定理）。
∴$\frac{CD}{CB}= \frac{CN}{CE}$。

2. 如图10,在$\triangle ABC$中,$CD是\angle ACB$的平分线,$DE// BC$,$AD:DB= 2:3$,$AC= 5$.求$DE$的长.

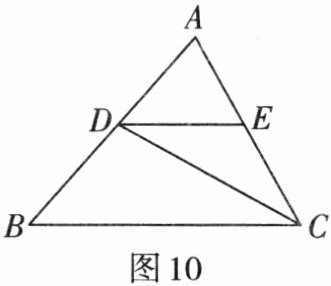
答案： 解：
∵ $DE // BC$，
∴ $\frac{AD}{AB} = \frac{AE}{AC}$，$\angle EDC = \angle DCB$。
∵ $AD:DB = 2:3$，设 $AD = 2k$，$DB = 3k$，则 $AB = 5k$，
∴ $\frac{AE}{AC} = \frac{AD}{AB} = \frac{2k}{5k} = \frac{2}{5}$。
∵ $AC = 5$，
∴ $AE = \frac{2}{5}AC = 2$，$EC = AC - AE = 5 - 2 = 3$。
∵ $CD$ 平分 $\angle ACB$，
∴ $\angle ECD = \angle DCB$，
∴ $\angle EDC = \angle ECD$，
∴ $DE = EC = 3$。
答：$DE$ 的长为 $3$。

3. 如图11,$\triangle ABC$是边长为2的等边三角形,$DE// BC$,$\triangle BCD的面积是\triangle ABC面积的\frac{1}{4}$.求$EC$的长.

答案： 1. 首先求$\triangle ABC$的面积：
已知$\triangle ABC$是边长$a = 2$的等边三角形，根据等边三角形面积公式$S=\frac{\sqrt{3}}{4}a^{2}$，可得$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^{2}=\sqrt{3}$。
2. 然后求$\triangle BCD$的面积：
因为$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$，所以$S_{\triangle BCD}=\frac{1}{4}×\sqrt{3}=\frac{\sqrt{3}}{4}$。
3. 接着求$\triangle DEC$的面积：
因为$DE// BC$，所以$\triangle ADE\sim\triangle ABC$，$\triangle DEC$与$\triangle BCD$等高（设高为$h$）。
又$S_{\triangle ADE}=S_{\triangle ABC}-S_{\triangle BCD}-S_{\triangle DEC}$，且$S_{\triangle ADE}=\frac{3}{4}S_{\triangle ABC}$（因为$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$，$S_{\triangle ADE}+S_{\triangle BCD}+S_{\triangle DEC}=S_{\triangle ABC}$，$DE// BC$，$\triangle ADE$与$\triangle ABC$的面积比等于相似比的平方，设$\frac{AD}{AB}=k$，则$\frac{S_{\triangle ADE}}{S_{\triangle ABC}} = k^{2}$，$S_{\triangle ADE}=\frac{3}{4}S_{\triangle ABC}$，$k^{2}=\frac{3}{4}$，$k = \frac{\sqrt{3}}{2}$，$\frac{AD}{AB}=\frac{AE}{AC}$）。
设$S_{\triangle DEC}=x$，因为$\triangle DEC$与$\triangle BCD$等高，根据三角形面积公式$S=\frac{1}{2}ah$（$a$为底，$h$为高），$\frac{S_{\triangle DEC}}{S_{\triangle BCD}}=\frac{DE}{BC}$（等高时，面积比等于底之比）。
由于$\triangle ADE\sim\triangle ABC$，$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{3}{4}$，则$\frac{DE}{BC}=\frac{\sqrt{3}}{2}$（由$S_{\triangle ADE}=\frac{3}{4}S_{\triangle ABC}$，$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\left(\frac{DE}{BC}\right)^{2}$）。
又$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$，$S_{\triangle ABC}=\sqrt{3}$，$S_{\triangle BCD}=\frac{\sqrt{3}}{4}$，且$\frac{S_{\triangle DEC}}{S_{\triangle BCD}}=\frac{DE}{BC}$，$S_{\triangle DEC}=\frac{3}{4}S_{\triangle BCD}$（因为$\frac{DE}{BC}=\frac{\sqrt{3}}{2}$，$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\frac{3}{4}$，$S_{\triangle ADE}+S_{\triangle BCD}+S_{\triangle DEC}=S_{\triangle ABC}$，$S_{\triangle ADE}=\frac{3}{4}S_{\triangle ABC}$，所以$S_{\triangle DEC}=\frac{3}{4}S_{\triangle BCD}$），$S_{\triangle DEC}=\frac{3}{16}\sqrt{3}$。
另一种方法：
因为$\triangle ABC$是边长为$2$的等边三角形，$S_{\triangle ABC}=\sqrt{3}$，$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}=\frac{\sqrt{3}}{4}$。
设$h$为$\triangle ABC$的高，$h=\sqrt{2^{2}-1^{2}}=\sqrt{3}$（根据勾股定理，等边三角形高$h=\sqrt{a^{2}-\left(\frac{a}{2}\right)^{2}}$，$a = 2$）。
设$DE = x$，$BC = 2$，$\triangle BCD$以$BC$为底的高$h_1$，$\triangle DEC$以$DE$为底的高$h_2$，$h_1 + h_2=h=\sqrt{3}$。
$S_{\triangle BCD}=\frac{1}{2}× BC× h_1$，$\frac{\sqrt{3}}{4}=\frac{1}{2}×2× h_1$，解得$h_1=\frac{\sqrt{3}}{4}$，则$h_2=\frac{3\sqrt{3}}{4}$。
因为$DE// BC$，$\triangle ADE\sim\triangle ABC$，$\frac{h - h_2}{h}=\frac{DE}{BC}$，$\frac{\sqrt{3}-\frac{3\sqrt{3}}{4}}{\sqrt{3}}=\frac{DE}{2}$，$DE=\frac{3}{2}$。
再根据$\triangle ADE\sim\triangle ABC$，$\frac{AE}{AC}=\frac{AD}{AB}$，$AC = 2$，设$EC=y$，$AE=2 - y$。
由$\triangle ADE\sim\triangle ABC$，$\frac{AE}{AC}=\frac{DE}{BC}$（相似三角形对应边成比例）。
已知$DE=\frac{3}{2}$，$BC = 2$，$AC = 2$，$\frac{2 - y}{2}=\frac{\frac{3}{2}}{2}$。
交叉相乘得$4-2y = 3$。
解得$y=\frac{1}{2}$。
解：
因为$\triangle ABC$是边长$a = 2$的等边三角形，根据等边三角形面积公式$S=\frac{\sqrt{3}}{4}a^{2}$，$S_{\triangle ABC}=\frac{\sqrt{3}}{4}×2^{2}=\sqrt{3}$。
已知$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$，所以$S_{\triangle BCD}=\frac{\sqrt{3}}{4}$。
由于$DE// BC$，$\triangle ADE\sim\triangle ABC$，$\frac{S_{\triangle ADE}}{S_{\triangle ABC}}=\left(\frac{DE}{BC}\right)^{2}$，$S_{\triangle ADE}=S_{\triangle ABC}-S_{\triangle BCD}-S_{\triangle DEC}$，且$S_{\triangle ADE}=\frac{3}{4}S_{\triangle ABC}$（因为$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$），则$\left(\frac{DE}{BC}\right)^{2}=\frac{3}{4}$，$DE=\sqrt{3}$（舍去）或$DE = \frac{\sqrt{3}}{2}× BC$（错误，重新来：
设$EC=x$，因为$DE// BC$，$\triangle ADE\sim\triangle ABC$，$\frac{AE}{AC}=\frac{AD}{AB}$。
由$S_{\triangle BCD}=\frac{1}{4}S_{\triangle ABC}$，$\triangle ABC$的高$h=\sqrt{2^{2}-1^{2}}=\sqrt{3}$，$S_{\triangle BCD}=\frac{1}{2}× BC× h_1$（$h_1$为$\triangle BCD$以$BC$为底的高），$\frac{\sqrt{3}}{4}=\frac{1}{2}×2× h_1$，得$h_1 = \frac{\sqrt{3}}{4}$，则$\triangle ADE$的高$h_2=h - h_1=\sqrt{3}-\frac{\sqrt{3}}{4}=\frac{3\sqrt{3}}{4}$。
又$\triangle ADE\sim\triangle ABC$，$\frac{h_2}{h}=\frac{AE}{AC}$（相似三角形对应高的比等于相似比），$\frac{\frac{3\sqrt{3}}{4}}{\sqrt{3}}=\frac{2 - x}{2}$。
即$\frac{3}{4}=\frac{2 - x}{2}$。
交叉相乘：$3×2 = 4×(2 - x)$。
$6 = 8-4x$。
$4x=2$。
解得$x=\frac{1}{2}$。
所以$EC$的长为$\boldsymbol{\frac{1}{2}}$。