《2025年新课程课堂同步练习册九年级数学上册华师大版》

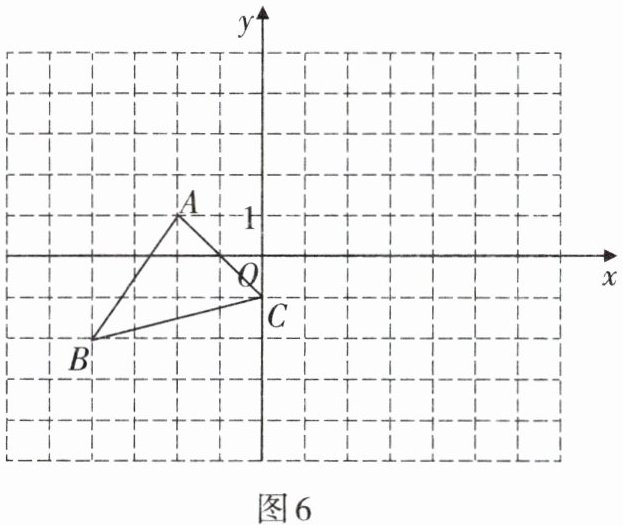
2. 将图6中的△ABC作下列运动,画出相应的图形,指出三个顶点的坐标所发生的变化.
(1)沿y轴负方向平移2个单位;
(2)关于y轴对称;
(3)以B点为位似中心,在现有网格中将△ABC放大到2倍.

答案： 解：由图6可得，△ABC三个顶点的坐标为：A(-2,1)，B(-4,-2)，C(0,-1)。
(1)沿y轴负方向平移2个单位，所得图形顶点坐标为：A1(-2,-1)，B1(-4,-4)，C1(0,-3)；变化规律：横坐标不变，纵坐标减2。
(2)关于y轴对称，所得图形顶点坐标为：A2(2,1)，B2(4,-2)，C2(0,-1)；变化规律：纵坐标不变，横坐标变为原来的相反数。
(3)以B点为位似中心，放大到2倍，所得图形顶点坐标为：A3(0,4)，B3(-4,-2)，C3(4,2)；变化规律：B点坐标不变，A、C点横、纵坐标均按位似比变化。

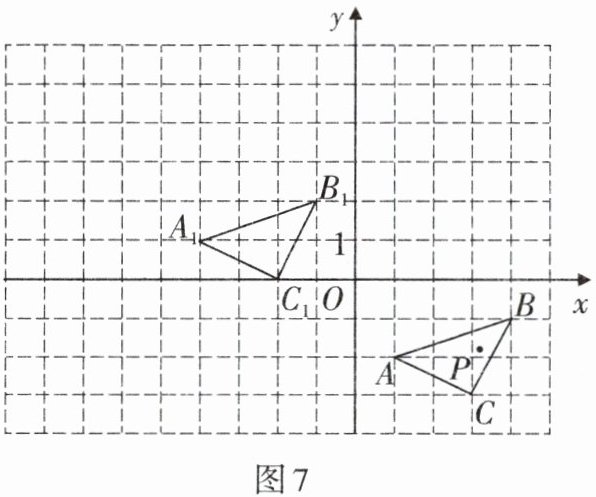
3. 如图7,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,-2),B(4,-1),C(3,-3),△ABC内部任意一点P的坐标为(a,b).
$(1)△A_1B_1C_1$是由△ABC经过某种变换后得到的图形,观察它们对应点的坐标之间的关系,指出是怎样变换得到的,并写出变换后点P的对应点$P_1$的坐标(用含a,b的代数式表示);
(2)以原点O为位似中心,在位似中心的同侧画出$△A_1B_1C_1$的一个位似图形$△A_2B_2C_2,$使它与$△A_1B_1C_1$的相似比为2:1. 写出$A_2,B_2,C_2$的坐标,及变换后点$P_1$的对应点$P_2$的坐标(用含a,b的代数式表示).

答案：
(1) 解：观察图形可知，△ABC与△A₁B₁C₁关于原点对称。
∵△ABC内部任意一点P的坐标为(a,b)，
∴变换后点P的对应点P₁的坐标为(-a,-b)。
(2) 解：
∵以原点O为位似中心，在位似中心的同侧画出△A₁B₁C₁的位似图形△A₂B₂C₂，相似比为2:1，
由图可得A₁(-3,1)，B₁(-1,2)，C₁(-2,0)，
∴A₂(-3×2,1×2)=(-6,2)，B₂(-1×2,2×2)=(-2,4)，C₂(-2×2,0×2)=(-4,0)。
∵点P₁的坐标为(-a,-b)，
∴变换后点P₁的对应点P₂的坐标为(-2a,-2b)。