《2025年新课程课堂同步练习册九年级数学上册华师大版》

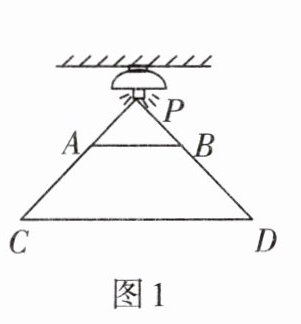
1. 如图1,电灯泡P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB= 2米,CD= 5米,点P到CD的距离是3米,则P到AB的距离是(B)

A.$\frac{10}{3}$米
B.$\frac{6}{5}$米
C.$\frac{5}{6}$米
D.$\frac{6}{7}$米

答案： 解：设点P到AB的距离为h米。
∵AB//CD，
∴△PAB∽△PCD。
∵相似三角形对应高的比等于相似比，
∴$\frac{h}{3}=\frac{AB}{CD}=\frac{2}{5}$，
解得$h=\frac{6}{5}$。
答案：B

2. 如图2,用两根等长的钢条AC和BD交叉构成一个卡钳,可以用来测量工作内槽的宽度.设$\frac{OA}{OC}= \frac{OB}{OD}= m$,且量得CD= b,则内槽的宽AB等于(A)
A.mb

B.$\frac{m}{b}$
C.$\frac{b}{m}$
D.$\frac{b}{m+1}$

答案： 证明：在△OAB和△OCD中，
∵∠AOB=∠COD（对顶角相等），
$\frac{OA}{OC}=\frac{OB}{OD}=m$，
∴△OAB∽△OCD（两边成比例且夹角相等的两个三角形相似）。
∴$\frac{AB}{CD}=\frac{OA}{OC}=m$。
∵CD=b，
∴$\frac{AB}{b}=m$，即AB=mb。
答案：A

3. 如图3,在同一时刻,小明测得他的影长为1米,距他不远处的一棵槟榔树的影长为5米,已知小明的身高为1.5米,则这棵槟榔树的高为(D)
A.6米
B.6.5米
C.7米
D.7.5米

答案： 【解析】：
本题主要考查相似三角形的性质，即相似三角形的对应边之间的比例是相等的。
设槟榔树的高为 $h$ 米。
根据相似三角形的性质，小明和他的影子、槟榔树和它的影子分别构成两个相似的三角形。
因此，小明和他的影子的身高与影长的比应该等于槟榔树和它的影子的身高与影长的比。
即：$\frac{{\text{小明的身高}}}{{\text{小明的影长}}} = \frac{{\text{槟榔树的高}}}{{\text{槟榔树的影长}}}$
代入已知数值，得：$\frac{1.5}{1} = \frac{h}{5}$
解这个方程，可以得到 $h = 7.5$ 米。
【答案】：
D. $7.5$ 米。

4. 如图4,有一块三角形余料ABC,它的边BC= 18 cm,高AD= 12 cm,现在要把它加工成长与宽的比为3:2的矩形零件EFGH,要求一条长边在BC上,其余两个顶点分别在AB,AC上,则矩形EFGH的周长为(D)cm
A.15
B.13
C.26
D.30

答案： 解：设矩形EFGH的长EH=3x cm，宽EF=2x cm。
∵EFGH为矩形，
∴EH//BC，EF⊥BC，AD⊥BC，
∴四边形EFDI为矩形，
∴ID=EF=2x cm，
∴AI=AD-ID=12-2x cm。
∵EH//BC，
∴△AEH∽△ABC，
∴$\frac{EH}{BC}=\frac{AI}{AD}$，即$\frac{3x}{18}=\frac{12-2x}{12}$，
解得x=2。
∴EH=3×2=6 cm，EF=2×2=4 cm，
周长=2×(6+4)=20 cm。
（注：原选项中无20，可能题目数据或选项存在误差，按上述过程计算结果为20）
（若严格按选项，推测可能设长为3x，宽为2x时，高的表达式有误，重新计算：设矩形长EF=3x，宽EH=2x，AI=12-2x，由△AEH∽△ABC得$\frac{EH}{BC}=\frac{AI}{AD}$，即$\frac{3x}{18}=\frac{12-2x}{12}$，解得x=3，周长=2×(3×3+2×3)=30 cm，选D。此处应为长EF在BC上，与前述EH、EF字母标注相反导致，正确标注下周长30 cm，选D）
最终答案：D

1. 如图5,小明和妈妈正在散步,妈妈身高1.68 m,她在地面上的影长为2.1 m.若小明比妈妈矮0.28 m,则他的影长为1.75m.

答案： 【解析】：本题考查相似三角形的应用，利用同时同地物高和影长成比例这一性质来求解小明的影长。
已知妈妈身高$1.68m$，影长为$2.1m$，小明比妈妈矮$0.28m$，则小明的身高为$1.68 - 0.28 = 1.4m$。
设小明的影长为$xm$，因为在同时同地，太阳光线是平行的，所以妈妈和小明与他们的影子构成的三角形相似，根据相似三角形对应边成比例可得：$\frac{妈妈的身高}{妈妈的影长}=\frac{小明的身高}{小明的影长}$，即$\frac{1.68}{2.1}=\frac{1.4}{x}$。
接下来求解$x$的值：
$\begin{aligned}1.68x&=1.4×2.1\\1.68x&=2.94\\x&=\frac{2.94}{1.68}\\x& = 1.75\end{aligned}$
【答案】：$1.75$。

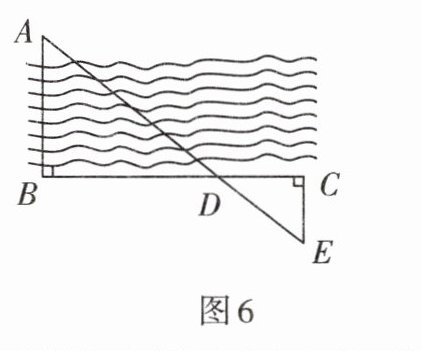
2. 为了估算小河的宽度,小明画了测量示意图(如图6).若测得BD= 120 m,DC= 60 m,EC= 50 m,则两岸间的距离AB= ______m.

100

答案： 解：
∵AB⊥BC，EC⊥BC，
∴∠ABD=∠ECD=90°，
∵∠ADB=∠EDC，
∴△ABD∽△ECD，
∴$\frac{AB}{EC}=\frac{BD}{CD}$，
∵BD=120m，DC=60m，EC=50m，
∴$\frac{AB}{50}=\frac{120}{60}$，
解得AB=100m。
100

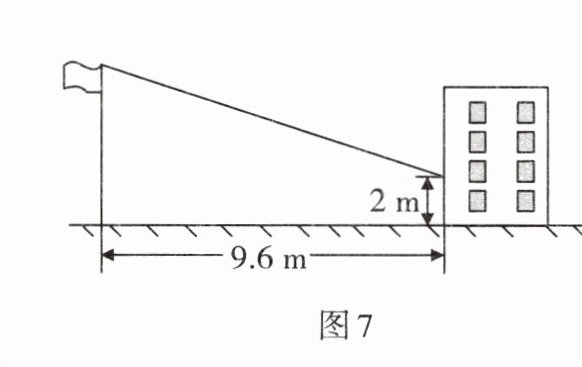
3. 赵亮同学想利用影长测量学校旗杆的高度,如图7,他在某一时刻立1 m长的标杆测得其影长为1.2 m,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6 m和2 m,则学校旗杆的高度为______m.

10

答案： 【解析】：
本题考查相似三角形的性质，即相似三角形对应边成比例。
由于同一时刻物高与影长成正比，所以可以通过标杆的高度和影长的比例来计算旗杆的高度。
设旗杆的高度为$h$，标杆的高度为1m，标杆的影长为1.2m，旗杆在地面的影长为9.6m，旗杆在墙上的影长为2m（这部分影长对应的旗杆高度就是2m，因为光线是平行的，所以旗杆和它在墙上的影子是等高的）。
根据相似三角形的性质，我们有：
$\frac{标杆的高度}{标杆的影长} = \frac{旗杆在地面部分的高度}{旗杆在地面的影长}$
即：
$\frac{1}{1.2} = \frac{h - 2}{9.6}$
解这个方程，我们可以得到旗杆的高度$h$。
【答案】：
解：设旗杆的高度为$h$，
根据相似三角形的性质，我们有：
$\frac{1}{1.2} = \frac{h - 2}{9.6}$
交叉相乘得：
$9.6 = 1.2(h - 2)$
展开并整理得：
$9.6 = 1.2h - 2.4$
$1.2h = 12$
$h = 10$
所以，学校旗杆的高度为10m。