《2025年新课程课堂同步练习册九年级数学上册华师大版》

1. 把下列方程化成一元二次方程的一般形式,并写出二次项系数、一次项系数和常数项:
(1)$x(x+1)-4(2x+3)= 0$;
(2)$(2x-1)(3x+2)= 6x-5$;
(3)$x(x-1)+3(x-1)= 0$;
(4)$x(x+3)= 2-x$.

答案： 【解析】：
本题主要考查一元二次方程的一般形式，即$ax^2 + bx + c = 0$（其中$a \neq 0$）的形式，并需要识别出二次项系数$a$，一次项系数$b$和常数项$c$。
对于每一个小题，我们首先将方程展开，然后合并同类项，最后整理成一般形式，并读出各项系数。
【答案】：
(1)解：
原方程：$x(x+1) - 4(2x+3) = 0$，
展开得：$x^2 + x - 8x - 12 = 0$，
整理得：$x^2 - 7x - 12 = 0$，
二次项系数为1，一次项系数为-7，常数项为-12。
(2)解：
原方程：$(2x-1)(3x+2) = 6x-5$，
展开得：$6x^2 + 4x - 3x - 2 = 6x - 5$，
整理得：$6x^2 - 5x + 3 = 0$，
二次项系数为6，一次项系数为-5，常数项为3。
(3)解：
原方程：$x(x-1) + 3(x-1) = 0$，
展开得：$x^2 - x + 3x - 3 = 0$，
整理得：$x^2 + 2x - 3 = 0$，
二次项系数为1，一次项系数为2，常数项为-3。
(4)解：
原方程：$x(x+3) = 2-x$，
展开得：$x^2 + 3x = 2 - x$，
整理得：$x^2 + 4x - 2 = 0$，
二次项系数为1，一次项系数为4，常数项为-2。

2. 某中学准备建一个面积为$375m^2$的矩形游泳池,且游泳池的宽比长短10 m. 求游泳池的长(要求:根据题意,列出方程,不必求解).

答案： 解：设游泳池的长为 $ x $ m，则宽为 $ (x - 10) $ m。
根据矩形面积公式，得 $ x(x - 10) = 375 $。

3. 某校团委准备举办学生绘画展览,为美化画面,在长为30 cm,宽为20 cm的矩形画面外面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原矩形的画面积相等(如图1),求彩纸的宽度(要求:根据题意,列出方程,不必求解).

答案： 【解析】：
首先，我们知道原矩形的长为$30\text{ cm}$，宽为$20 \text{ cm}$，所以原矩形的面积为$30 × 20 = 600 \text{ cm}^2$。
设彩纸的宽度为$x \text{ cm}$，那么镶上彩纸后，矩形的长变为$(30 + 2x) \text{ cm}$，宽变为$(20 + 2x) \text{ cm}$。
根据题意，彩纸的面积恰好与原矩形的面积相等，所以新矩形的面积是原矩形面积的2倍，即$2 × 600 = 1200 \text{ cm}^2$。
因此，我们可以列出方程$(30 + 2x)(20 + 2x) = 1200$。
【答案】：
方程为$(30 + 2x)(20 + 2x) = 1200$。

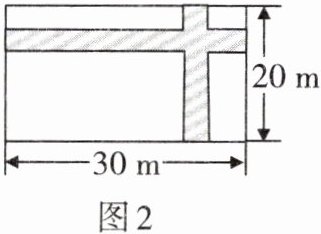
4. 在宽为20米,长为30米的矩形地面上修建两条同样宽的道路(如图2),余下部分作为耕地. 若耕地面积需要$551米^2$,求修建的路宽(要求:根据题意,列出方程,不必求解).

答案： 【解析】：
题目给出矩形地面的长和宽，以及耕地面积，要求列出关于路宽的方程，本题可通过设路宽为$x$米，根据矩形面积公式，利用平移性质得到耕地面积的表达式，进而列出方程，考查了一元二次方程的运用。
设修建的路宽为$x$米。
根据平移性质，将道路平移到矩形的边缘，此时耕地面积可看作是一个新的矩形的面积，新矩形的长为$(30 - x)$米，宽为$(20 - x)$米。
已知耕地面积需要$551$平方米，根据矩形面积公式$S = 长×宽$，可列出方程$(30 - x)(20 - x) = 551$。
【答案】：
设修建的路宽为$x$米，根据题意可列方程为$(30 - x)(20 - x) = 551$。