25. (12 分)如图,在 Rt△ABC 中,∠ACB = 90°,∠ABC = 30°,将△ABC 绕点 B 顺时针旋转一定的角度 α 得到△DBE,点 A,C 的对应点分别是点 D,E.
(1)根据题意可知∠DBE = ______;
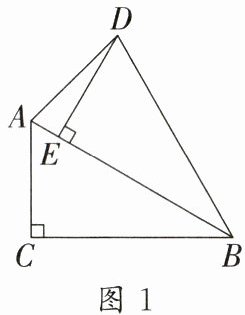
(2)如图 1,连接 AD,当点 E 恰好在 AB 上时,求∠ADE 的度数;
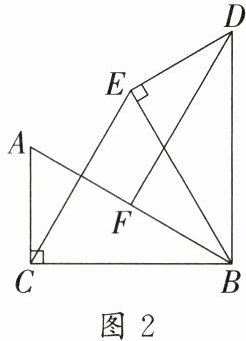
(3)如图 2,若 α = 60°,F 是 AB 的中点,连接 CE,DF,判断 DF 和 CE 是否相等,并证明你的结论.
(1)根据题意可知∠DBE = ______;
(2)如图 1,连接 AD,当点 E 恰好在 AB 上时,求∠ADE 的度数;
(3)如图 2,若 α = 60°,F 是 AB 的中点,连接 CE,DF,判断 DF 和 CE 是否相等,并证明你的结论.


答案:
解:
(1)由旋转的性质,可得∠DBE=∠ABC =30°.
故答案为:30°
(2)因为△DBE是由△ABC旋转得到,
所以AB=BD,∠ABD=∠ABC=30°,∠ACB=∠BED=90°,
所以∠BAD=∠BDA=$\frac{180° - ∠ABD}{2}$=75°,
所以∠ADE=∠BED-∠BAD=15°.
(3)DF=CE.
证明:连接CF.

因为F是AB的中点,∠ACB=90°,∠ABC=30°,
所以CF=$\frac{1}{2}$AB=AF=BF=AC,∠A=60°.
因为△DBE由△ABC旋转60°得到,
所以∠CBE=∠ABD=60°,BC=BE,AB =DB,
所以△CBE为等边三角形,
所以CE=BC=BE.
在△ABC和△BDF中,
AB=BD,
∠A=∠ABD=60°,
AC=BF,
所以△ABC≌△BDF(SAS),
所以BC=DF,
所以DF=CE.
解:
(1)由旋转的性质,可得∠DBE=∠ABC =30°.
故答案为:30°
(2)因为△DBE是由△ABC旋转得到,
所以AB=BD,∠ABD=∠ABC=30°,∠ACB=∠BED=90°,
所以∠BAD=∠BDA=$\frac{180° - ∠ABD}{2}$=75°,
所以∠ADE=∠BED-∠BAD=15°.
(3)DF=CE.
证明:连接CF.

因为F是AB的中点,∠ACB=90°,∠ABC=30°,
所以CF=$\frac{1}{2}$AB=AF=BF=AC,∠A=60°.
因为△DBE由△ABC旋转60°得到,
所以∠CBE=∠ABD=60°,BC=BE,AB =DB,
所以△CBE为等边三角形,
所以CE=BC=BE.
在△ABC和△BDF中,
AB=BD,
∠A=∠ABD=60°,
AC=BF,
所以△ABC≌△BDF(SAS),
所以BC=DF,
所以DF=CE.
查看更多完整答案,请扫码查看


