《2025年新坐标同步练习九年级数学上册人教版青海专用》

7. 如图,抛物线 $ y_1 = ax^2 + bx + c $ 与 $ x $ 轴交于点 $ A(-2,0) $,$ B(6,0) $,与 $ y $ 轴交于点 $ C $,直线 $ y_2 = mx + c $ 经过点 $ B $. 以下结论错误的是( )


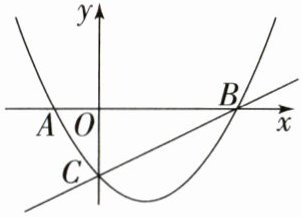
A.$ b^2 - 4ac ＞ 0 $
B.关于 $ x $ 的方程 $ ax^2 + bx = mx $ 有两个解是 $ x_1 = 0 $,$ x_2 = 6 $
C.若 $ y_1 \leq c $,则 $ 0 \leq x \leq 4 $
D.关于 $ x $ 的不等式 $ ax^2 + bx ＞ mx $ 的解集是 $ 0 ＜ x ＜ 6 $

答案： 解析:选D。A.根据抛物线与$x$轴有两个交点可知$b^{2}-4ac＞0$，故A正确；
B.根据抛物线与一次函数图象交于B，C两点，可得关于$x$的方程$ax^{2}+bx = mx$的解为$x_1 = 0$，$x_2 = 6$，故B正确；
C.抛物线$y_1 = ax^{2}+bx + c$与$x$轴交于点$A(-2,0)$，$B(6,0)$，所以对称轴为$x = \frac{-2 + 6}{2}=2$，所以点C关于对称轴的对称点的横坐标为4，所以若$y_1\leqslant c$，则$0\leqslant x\leqslant4$，故C正确；
D.由图象可知，关于$x$的不等式$ax^{2}+bx＞mx$的解集是$x＜0$或$x＞6$，故D错误。故选D。

8. 二次函数 $ y = ax^2 + bx + c $ 的 $ y $ 与 $ x $ 的部分对应值如下表:
| $ x $ | $ - 1 $ | $ 0 $ | $ 1 $ | $ 3 $ |
| $ y $ | $ 0 $ | $ - 1.5 $ | $ - 2 $ | $ 0 $ |

根据表格中的信息,得到了如下的结论:
① $ abc ＜ 0 $;
②二次函数 $ y = ax^2 + bx + c $ 可改写为 $ y = a(x - 1)^2 - 2 $ 的形式;
③关于 $ x $ 的一元二次方程 $ ax^2 + bx + c = - 1.5 $ 的根为 $ x_1 = 0 $,$ x_2 = 2 $;
④若 $ y ＞ 0 $,则 $ x ＞ 3 $;
⑤当 $ x \geq 2 $ 时,$ y $ 有最小值是 $ - 1.5 $.
其中所有正确结论的序号是( )

A.①②④
B.②③⑤
C.①③⑤
D.②③④⑤

答案： B

9. 已知函数 $ y = (m - 3)x^{m^2 - 7} $ 是二次函数,则 $ m = $______.

答案： 解析:因为函数$y=(m - 3)x^{m^{2}-7}$是二次函数，所以$m - 3\neq0$且$m^{2}-7 = 2$，解得$m = -3$。
　答案:$-3$

10. 一个二次函数的图象的顶点坐标为 $ (3, - 1) $,与 $ y $ 轴的交点坐标为 $ (0, - 4) $,则这个二次函数的解析式是______.

答案： 解析:设二次函数的解析式为$y = a(x - 3)^{2}-1$，把$(0,-4)$代入，得$a\cdot(0 - 3)^{2}-1 = -4$，解得$a = -\frac{1}{3}$，
　所以这个二次函数的解析式为$y = -\frac{1}{3}(x - 3)^{2}-1 = -\frac{1}{3}x^{2}+2x - 4$。
　答案:$y = -\frac{1}{3}x^{2}+2x - 4$

11. 若二次函数 $ y = x^2 - 4x + n $ 的图象与 $ x $ 轴只有一个公共点,则实数 $ n = $______.

答案： 4

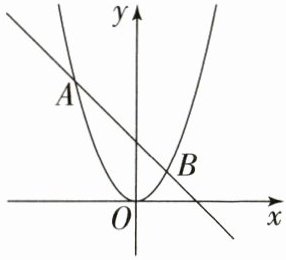
12. 如图,抛物线 $ y = ax^2 $ 与直线 $ y = bx + c $ 的两个交点分别为 $ A(-2,4) $,$ B(1,1) $,则关于 $ x $ 的方程 $ ax^2 = bx + c $ 的解是______.

答案： $x_1 = -2$，$x_2 = 1$

13. 如图,抛物线 $ y_1 = ax^2 + bx + c $ 与直线 $ y_2 = mx + n $ 相交于点 $ (3,0) $ 和 $ (0,3) $. 若 $ ax^2 + bx + c ＞ mx + n $,则 $ x $ 的取值范围是______.

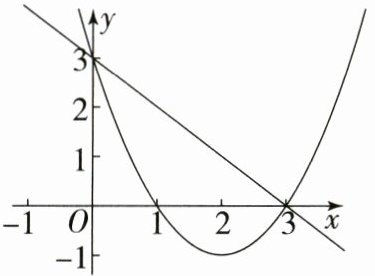
答案： $x＜0$或$x＞3$