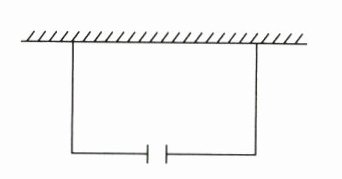
19. (6分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为 $ 29 $ 米的篱笆围成.已知墙长为 $ 18 $ 米,为方便进入,在墙的对面留出 $ 1 $ 米宽的门(如图所示).怎样围成面积为 $ 100 $ 平方米的苗圃园?

答案:
解:设这个苗圃园垂直于墙的一边长为x米,则这个苗圃园平行于墙的一边长为(29-2x+1)米.根据题意,得x(29-2x+1)=100,解得x₁=5,x₂=10.因为当x=5时,29-2x+1=20>18,故舍去,所以x=10.所以29-2x+1=10,所以这个苗圃园垂直于墙的一边长为10米,平行于墙的一边长为10米.答:这个苗圃园垂直于墙的一边长为10米,平行于墙的一边长为10米时,可以围成面积为100平方米的苗圃园.
20. (7分)定义:方程 $ ax^{2}+bx + c = 0 $ 是一元二次方程 $ cx^{2}+bx + a = 0 $ 的倒方程.
(1)已知 $ x = 4 $ 是 $ x^{2}+4x + c = 0 $ 的倒方程的解,求 $ c $ 的值;
(2)一元二次方程 $ ax^{2}-4x + c = 0 $ 的倒方程只有一个解为 $ x = -1 $,求一元二次方程 $ ax^{2}-4x + c = 0 $ 的解.
(1)已知 $ x = 4 $ 是 $ x^{2}+4x + c = 0 $ 的倒方程的解,求 $ c $ 的值;
(2)一元二次方程 $ ax^{2}-4x + c = 0 $ 的倒方程只有一个解为 $ x = -1 $,求一元二次方程 $ ax^{2}-4x + c = 0 $ 的解.
答案:
20.解:
(1)方程x²+4x+c=0的倒方程为cx²+4x+1=0,把x=4代入,得16c+4×4+1=0,解得c=-$\frac{17}{16}$.
(2)一元二次方程ax²-4x+c=0的倒方程为cx²-4x+a=0,而倒方程只有一个解,所以c=0,即-4x+a=0.因为x=-1是方程-4x+a=0的解,代入,得a=-4,所以一元二次方程ax²-4x+c=0为-4x²-4x=0,解得x₁=0,x₂=-1.
(1)方程x²+4x+c=0的倒方程为cx²+4x+1=0,把x=4代入,得16c+4×4+1=0,解得c=-$\frac{17}{16}$.
(2)一元二次方程ax²-4x+c=0的倒方程为cx²-4x+a=0,而倒方程只有一个解,所以c=0,即-4x+a=0.因为x=-1是方程-4x+a=0的解,代入,得a=-4,所以一元二次方程ax²-4x+c=0为-4x²-4x=0,解得x₁=0,x₂=-1.
查看更多完整答案,请扫码查看


