《2025年新坐标同步练习九年级数学上册人教版青海专用》

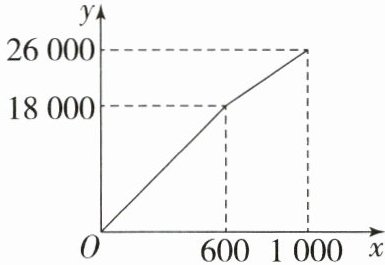
24. (11 分)为了“创建文明城市,建设美丽家园”,某市某社区将辖区内的一块面积为 $ 1000 m^2 $ 的空地进行绿化,一部分种草,剩余部分栽花. 设种草部分的面积为 $ x(m^2) $,种草所需费用 $ y_1 $(元)与 $ x(m^2) $ 之间的函数关系式为 $ y_1 = \left\{\begin{array}{ll}k_1x(0 \leq x ＜ 600), \\ k_2x + b(600 \leq x \leq 1000),\end{array} \right. $ 其图象如图所示:

栽花所需费用 $ y_2 $(元)与 $ x(m^2) $ 之间的函数关系式为 $ y_2 = - 0.01x^2 - 20x + 30000(0 \leq x \leq 1000) $.
(1)请直接写出 $ k_1 $,$ k_2 $ 和 $ b $ 的值;
(2)设这块 $ 1000 m^2 $ 空地的绿化总费用为 $ W $(元),请利用 $ W $ 与 $ x $ 之间的函数关系式,求出绿化总费用 $ W $ 的最大值;
(3)若种草部分的面积不少于 $ 700 m^2 $,栽花部分的面积不少于 $ 100 m^2 $,请求出绿化总费用 $ W $ 的最小值.

答案： 解:
(1)$k_1 = 30$，$k_2 = 20$，$b = 6000$。
(2)当$0\leqslant x＜600$时，
　　$W = 30x + (-0.01x^{2}-20x + 30000)=-0.01x^{2}+10x + 30000=-0.01(x - 500)^{2}+32500$。
　　因为$-0.01＜0$，
　　所以当$x = 500$时，
$W$取得最大值，为$32500$元；
　　当$600\leqslant x\leqslant1000$时，
$W = 20x + 6000 + (-0.01x^{2}-20x + 30000)=-0.01x^{2}+36000$。
　　因为$-0.01＜0$，
所以当$600\leqslant x\leqslant1000$时，$W$随$x$的增大而减小，
所以当$x = 600$时，
$W$取得最大值，为$32400$元。
　　因为$32400＜32500$，
所以$W$的最大值为$32500$元。
(3)由题意，得$1000 - x\geqslant100$，解得$x\leqslant900$，又因为$x\geqslant700$，所以$700\leqslant x\leqslant900$。
　　因为当$700\leqslant x\leqslant900$时，$W$随$x$的增大而减小，
所以当$x = 900$时，$W_{最小}=-0.01×900^{2}+36000 = 27900$，
即$W$的最小值为$27900$元。
　答:绿化总费用$W$的最小值为$27900$元。