14. 在二次函数 $ y = x^2 - 2x - 3 $ 中,当 $ 0 \leq x \leq 3 $ 时,设 $ y $ 的最大值为 $ y_1 $,$ y $ 的最小值为 $ y_2 $,则 $ y_1 - y_2 = $______.
答案:
4
15. 某电商平台销售某款儿童组装玩具,进价为每件 100 元,在销售过程中发现,每周的销售量 $ y $(件)与每件玩具的售价 $ x $(元)之间满足一次函数关系:$ y = - 2x + 320 $(其中 $ 100 \leq x \leq 120 $,且 $ x $ 为整数),该电商平台每周销售这款玩具所获得的最大利润为______元.
答案:
1600
16. 如图,在平面直角坐标系中,点 $ A $ 在抛物线 $ y = \frac{1}{2}x^2 - 2x + 3 $ 上运动,过点 $ A $ 作 $ AC \perp x $ 轴于点 $ C $,以 $ AC $ 为对角线作矩形 $ ABCD $,连接 $ BD $,则对角线 $ BD $ 的最小值为______.
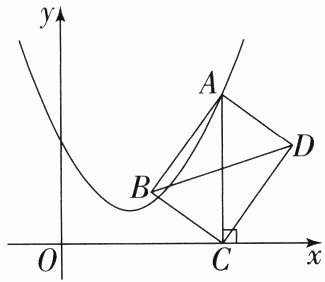

答案:
解析:$y = \frac{1}{2}x^{2}-2x + 3 = \frac{1}{2}(x - 2)^{2}+1$,
则抛物线的顶点坐标为$(2,1)$,
所以当点A在抛物线的顶点上时,AC最小,最小值为1。
因为四边形ABCD是矩形,
所以$AC = BD$,
所以对角线BD的最小值为1。
答案:1
则抛物线的顶点坐标为$(2,1)$,
所以当点A在抛物线的顶点上时,AC最小,最小值为1。
因为四边形ABCD是矩形,
所以$AC = BD$,
所以对角线BD的最小值为1。
答案:1
17. (6 分)已知二次函数 $ y = - 2x^2 + bx + c $ 的图象经过 $ A(-1,0) $,$ B(3,0) $ 两点,求二次函数的解析式.
答案:
解:把$(-1,0)$,$(3,0)$代入$y = -2x^{2}+bx + c$,得$\begin{cases}-2 - b + c = 0 \\ -18 + 3b + c = 0 \end{cases}$,
解得$\begin{cases}b = 4 \\ c = 6 \end{cases}$,
所以二次函数的解析式为$y = -2x^{2}+4x + 6$。
解得$\begin{cases}b = 4 \\ c = 6 \end{cases}$,
所以二次函数的解析式为$y = -2x^{2}+4x + 6$。
18. (6 分)若二次函数 $ y = - x^2 + 2x + k $ 的图象与 $ x $ 轴有两个交点,求 $ k $ 的取值范围.
答案:
解:因为二次函数$y = -x^{2}+2x + k$的图象与$x$轴有两个交点,
所以$\Delta = 4 - 4×(-1)\cdot k>0$,
解得$k> -1$,
所以$k$的取值范围为$k> -1$。
所以$\Delta = 4 - 4×(-1)\cdot k>0$,
解得$k> -1$,
所以$k$的取值范围为$k> -1$。
查看更多完整答案,请扫码查看


