《2025年暑假生活八年级数学河北少年儿童出版社》

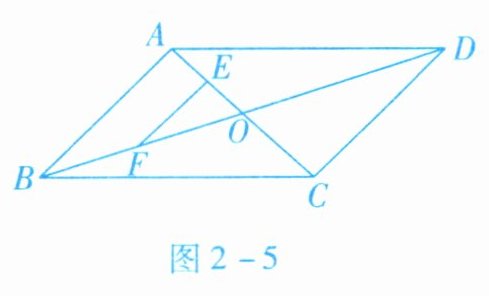
5. 如图2-5所示,$□ ABCD的对角线AC$,$BD相交于点O$,点$E$,$F分别是线段AO$,$BO$的中点. 若$AC + BD = 24cm$,$\triangle AOB$的周长是18cm,则$EF= $3cm.

答案： 【解析】：因为四边形$ABCD$是平行四边形，所以对角线互相平分，即$AO = \frac{1}{2}AC$，$BO=\frac{1}{2}BD$。已知$AC + BD=24\,\text{cm}$，则$AO + BO=\frac{1}{2}(AC + BD)=\frac{1}{2}×24 = 12\,\text{cm}$。
又因为$\triangle AOB$的周长是$18\,\text{cm}$，即$AO + BO+AB = 18\,\text{cm}$，所以$AB=18-(AO + BO)=18 - 12=6\,\text{cm}$。
点$E$、$F$分别是线段$AO$、$BO$的中点，所以$EF$是$\triangle AOB$的中位线。根据三角形中位线定理，三角形的中位线平行于第三边且等于第三边的一半，因此$EF=\frac{1}{2}AB=\frac{1}{2}×6 = 3\,\text{cm}$。
【答案】：3cm

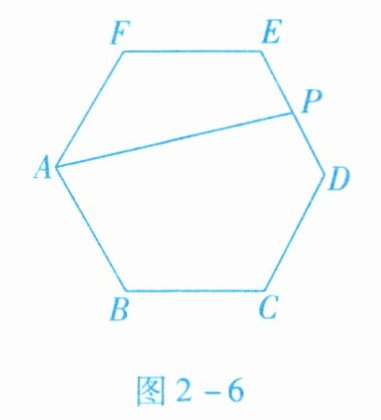
1. 如图2-6所示,正六边形$ABCDEF$中,$AB = 2$,点$P是ED$的中点,连接$AP$,则$AP$的长为 (C)

A.$2\sqrt{3}$
B.4
C.$\sqrt{13}$
D.$\sqrt{11}$

答案： 【解析】：
连接AE,
正六边形$ABCDEF$中，$\angle F=\angle FAB=120^\circ$，$FA=FE=AB=2$，
$\therefore \angle FAE=\angle FEA=30^\circ$，
$\therefore \angle EAB=\angle FAB-\angle FAE=120^\circ-30^\circ=90^\circ$，
$\therefore AE=\sqrt{3}AB=2\sqrt{3}$，
$\because$点P是ED的中点，
$\therefore EP=\frac{1}{2}ED=1$，
在$Rt\triangle AEP$中，根据勾股定理可得
$AP=\sqrt{AE^2+EP^2}=\sqrt{(2\sqrt{3})^2+1^2}=\sqrt{13}$。
【答案】：C

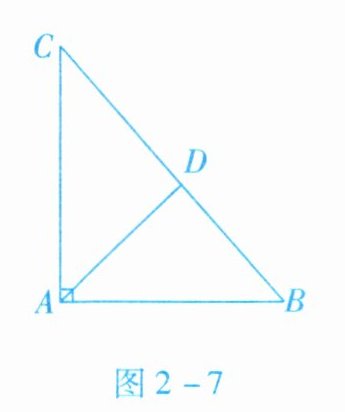
2. 如图2-7所示,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AB = 3$,$AC = 4$,$AD平分\angle BAC交BC于点D$,则$BD$的长为 (A)

A.$\frac{15}{7}$
B.$\frac{12}{5}$
C.$\frac{20}{7}$
D.$\frac{21}{5}$

答案： 【解析】：
首先，根据勾股定理，在直角三角形ABC中，有
$BC = \sqrt{AB^2 + AC^2} = \sqrt{3^2 + 4^2} = 5$，
由于AD平分$\angle BAC$，根据角平分线的性质，有
$\frac{BD}{DC} = \frac{AB}{AC} = \frac{3}{4}$，
设$BD = 3x$，$DC = 4x$，则
$BC = BD + DC = 3x + 4x = 7x = 5$，
解得$x = \frac{5}{7}$，
所以$BD = 3x = \frac{15}{7}$。
【答案】：A

3. 在下列给定的条件中,能画出平行四边形的是 (B)
A.以16cm,20cm为对角线,18cm为一边
B.以40cm,56cm为对角线,36cm为一边
C.以80cm为一条对角线,40cm,32cm为两条邻边
D.以12cm为一条对角线,6cm,18cm为两条邻边

答案： 【解析】：要判断能否画出平行四边形，可依据平行四边形的性质：平行四边形的对角线互相平分，且两条对角线的一半与一边构成三角形，需满足三角形三边关系（任意两边之和大于第三边，任意两边之差小于第三边）；对于已知一条对角线和两条邻边的情况，两条邻边与对角线也需构成三角形，同样满足三角形三边关系。
选项A：对角线长16cm、20cm，则对角线一半分别为8cm、10cm，与边18cm。判断8+10=18，不满足三角形两边之和大于第三边（18不大于18），故不能构成三角形，无法画出平行四边形。
选项B：对角线长40cm、56cm，对角线一半分别为20cm、28cm，与边36cm。验证三角形三边关系：20+28=48＞36，28+36=64＞20，20+36=56＞28；且28-20=8＜36，36-28=8＜20，36-20=16＜28，均满足，能构成三角形，可画出平行四边形。
选项C：对角线80cm，邻边40cm、32cm。判断40+32=72＜80，不满足三角形两边之和大于第三边，无法构成三角形，不能画出平行四边形。
选项D：对角线12cm，邻边6cm、18cm。判断6+12=18，不满足三角形两边之和大于第三边（18不大于18），无法构成三角形，不能画出平行四边形。
综上，只有选项B符合条件。
【答案】：B

4. 在$\triangle ABC$中,$AB = 17$,$BC = 30$,$BC边上的中线AD = 8$,则$\triangle ABC$的形状是 (B)
A.直角三角形
B.等腰三角形
C.等边三角形
D.等腰直角三角形

答案： 【解析】：
首先，根据题目条件，我们知道在$\triangle ABC$中，$AB = 17$，$BC = 30$，$BC$边上的中线$AD = 8$。
由于$AD$是$BC$的中线，根据中线的性质，我们有$BD = \frac{BC}{2} = 15$。
接下来，我们可以利用勾股定理的逆定理来判断$\triangle ABD$的形状。
计算得：$AB^{2} = 17^{2} = 289$，$BD^{2} + AD^{2} = 15^{2} + 8^{2} = 225 + 64 = 289$。
由于$AB^{2} = BD^{2} + AD^{2}$，根据勾股定理的逆定理，我们可以得出$\triangle ABD$是直角三角形，且$\angle ADB = 90^{\circ}$。
然后，由于$AD$是$BC$的中线，且$\angle ADB = 90^{\circ}$，我们可以推断出$AD$也是$BC$的垂直平分线。
根据垂直平分线的性质，我们知道$AB = AC$。
因此，$\triangle ABC$是等腰三角形。
【答案】：B