《2025年暑假生活八年级数学河北少年儿童出版社》

1. 计算：$\sqrt{2} × \sqrt{6} = $$2\sqrt{3}$.

答案： 【解析】：根据二次根式乘法法则，$\sqrt{a} × \sqrt{b} = \sqrt{ab}$（$a\geq0$，$b\geq0$），则$\sqrt{2} × \sqrt{6} = \sqrt{2×6} = \sqrt{12}$。又因为$\sqrt{12} = \sqrt{4×3} = \sqrt{4}×\sqrt{3} = 2\sqrt{3}$。
【答案】：$2\sqrt{3}$

2. 直角三角形两直角边长分别是$5\mathrm{cm}$,$12\mathrm{cm}$,则斜边上的高为$\frac{60}{13}\mathrm{cm}$.

答案： 【解析】：
首先，根据勾股定理，直角三角形的斜边长度 $c$ 可以通过两直角边长 $a$ 和 $b$ 计算得出：
$c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm}$，
设斜边上的高为 $h$ cm。
根据直角三角形的面积公式，面积 $S$ 可以用两种方式表示：
$S = \frac{1}{2} × a × b = \frac{1}{2} × 5 × 12 = 30 \text{ cm}^2$，
$S = \frac{1}{2} × c × h$，
由于两种方式表示的面积必须相等，因此有：
$\frac{1}{2} × 13 × h = 30$，
解这个方程，得到：
$h = \frac{60}{13} \text{ cm}$。
【答案】：$\frac{60}{13} \text{ cm}$。

3. 已知正比例函数$y = kx(k \neq 0)$,点$(2,-3)$在该函数的图象上,则$y随x$的增大而减小.(填“增大”或“减小”)

答案： 【解析】：因为点$(2,-3)$在正比例函数$y = kx(k \neq 0)$的图象上，所以将$x=2$，$y=-3$代入函数可得$-3 = 2k$，解得$k=-\frac{3}{2}$。由于$k=-\frac{3}{2} ＜ 0$，根据正比例函数的性质，当$k ＜ 0$时，$y$随$x$的增大而减小。
【答案】：减小

4. 已知在一个样本中,$40个数据分别落在4$个组内,第一、二、四组数据个数分别为$5$,$12$,$8$,则第三组的频数为15.

答案： 【解析】：
已知样本中总共有40个数据，且这些数据分布在4个组内。
第一组有5个数据，第二组有12个数据，第四组有8个数据。
设第三组的数据个数为$x$，则根据总数据个数，可以列出等式：
$5 + 12 + x + 8 = 40$，
解这个等式，得到：
$x = 40 - 5 - 12 - 8 = 15$，
所以，第三组的频数为15。
【答案】：15

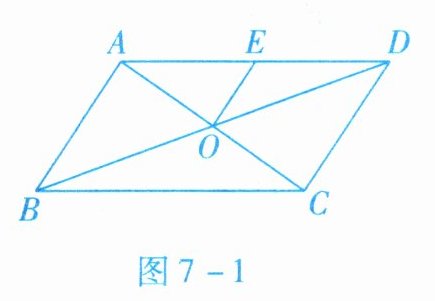
5. 如图$7 - 1$所示,在$□ ABCD$中,$AC与BD相交于点O$,点$E是AD$的中点,$AC = 6\mathrm{cm}$,$BD = 8\mathrm{cm}$,$OE = 1.75\mathrm{cm}$,$\triangle OCD$的周长是____10.5$\mathrm{cm}$.

答案： 【解析】：在平行四边形$ABCD$中，对角线$AC$与$BD$相交于点$O$，根据平行四边形对角线互相平分的性质，可得$OA = OC=\frac{1}{2}AC$，$OB = OD=\frac{1}{2}BD$。已知$AC = 6\space cm$，$BD = 8\space cm$，所以$OC=\frac{1}{2}×6 = 3\space cm$，$OD=\frac{1}{2}×8=4\space cm$。
点$E$是$AD$的中点，$O$是$BD$的中点，所以在$\triangle ABD$中，$OE$是中位线，根据三角形中位线定理，中位线平行于第三边且等于第三边的一半，可得$OE=\frac{1}{2}AB$。已知$OE = 1.75\space cm$，则$AB=2OE=2×1.75 = 3.5\space cm$。
因为平行四边形的对边相等，所以$CD = AB=3.5\space cm$。
$\triangle OCD$的周长为$OC + OD+CD=3 + 4+3.5=10.5\space cm$。
【答案】：10.5

1. 顺次连接菱形各边中点所得到的四边形是(A)
A.矩形
B.菱形
C.正方形
D.平行四边形

答案： 【解析】：
首先，给定一个菱形，我们知道菱形的对角线是互相垂直且平分的。
设菱形为$ABCD$，其中点分别为$E, F, G, H$，即$E$是$AB$的中点，$F$是$BC$的中点，$G$是$CD$的中点，$H$是$DA$的中点。
连接菱形的对角线$AC$和$BD$，它们会相交于点$O$。
由于$E$和$F$分别是$AB$和$BC$的中点，根据三角形的中位线性质，我们有$EF // AC$且$EF = \frac{1}{2}AC$。
同理，$GH // AC$且$GH = \frac{1}{2}AC$，所以$EF // GH$且$EF = GH$。
同样地，我们可以证明$EH // FG$且$EH = FG$。
接下来，我们需要证明这个四边形的内角有一个是直角。
由于菱形的对角线互相垂直，即$AC \perp BD$，而$EF // AC$且$EH // BD$，所以$EF \perp EH$。
综上，我们证明了顺次连接菱形各边中点所得到的四边形是一个矩形。
【答案】：A

2. 图$7 - 2$是八年级(1)班参加课外兴趣小组人数的扇形统计图,则表示唱歌兴趣小组人数的扇形的圆心角度数是(B)

A.$36^{\circ}$
B.$72^{\circ}$
C.$108^{\circ}$
D.$180^{\circ}$

答案： 【解析】：
扇形统计图中，圆心角度数是根据各部分占总体的百分比来计算的。
根据题意，参加唱歌兴趣小组的人数占总人数的比例为：
$1 - 50\% - 30\% = 20\%$。
整个圆为$360^{\circ}$，所以唱歌兴趣小组人数的扇形圆心角度数为：
$360^{\circ} × 20\% = 72^{\circ}$。
【答案】：B

3. 如图$7 - 3$所示,在菱形$ABCD$中,$\angle B = 60^{\circ}$,$AB = 4$,则以$AC为边长的正方形ACEF$的周长为(C)

A.$14$
B.$15$
C.$16$
D.$17$

答案： 【解析】：
因为四边形$ABCD$是菱形，所以$AB=BC$。
由于$\angle B=60^\circ$，所以$\triangle ABC$是等边三角形。
因此，$AC=AB=4$。
以$AC$为边长的正方形$ACEF$，其每条边长都是$4$。
正方形的周长为边长的四倍，即$4 × 4 = 16$。
【答案】：C