《2025年暑假生活八年级数学河北少年儿童出版社》

3. 如图$10 - 2$所示,$P _ { 1 }$,$P _ { 2 }$,$P _ { 3 }$这三个点中,在第二象限内的是(D)

A.$P _ { 1 }$,$P _ { 2 }$,$P _ { 3 }$
B.$P _ { 1 }$,$P _ { 2 }$
C.$P _ { 1 }$,$P _ { 3 }$
D.$P _ { 1 }$

答案： 【解析】：在平面直角坐标系中，第二象限内点的坐标特征是横坐标为负，纵坐标为正。
观察图中$P_1$：位于$x$轴负半轴左侧、$y$轴正半轴上方，横坐标为负，纵坐标为正，符合第二象限特征。
$P_2$：位于$y$轴正半轴上，横坐标为$0$，不属于任何象限。
$P_3$：位于$x$轴负半轴上，纵坐标为$0$，不属于任何象限。
因此，只有$P_1$在第二象限。
【答案】：D

4. 下列函数中,$y随x$的增大而减小的函数是(C)
A.$y = 2 x + 8$
B.$y = 4 x - 2$
C.$y = - 2 x + 8$
D.$y = 4 x$

答案： 【解析】：对于一次函数$y = kx + b$（$k$，$b$为常数，$k≠0$），当$k＞0$时，$y$随$x$的增大而增大；当$k＜0$时，$y$随$x$的增大而减小。
选项A：$y = 2x + 8$，其中$k = 2＞0$，所以$y$随$x$的增大而增大，不符合题意。
选项B：$y = 4x - 2$，其中$k = 4＞0$，所以$y$随$x$的增大而增大，不符合题意。
选项C：$y = -2x + 8$，其中$k = -2＜0$，所以$y$随$x$的增大而减小，符合题意。
选项D：$y = 4x$，其中$k = 4＞0$，所以$y$随$x$的增大而增大，不符合题意。
【答案】：C

5. 全国人口普查时,人口调查采用普查方式的理由是(A)
A.人口调查需要获得全面准确的信息
B.人口调查的数目不太大
C.人口调查具有破坏性
D.受条件限制,无法进行抽样调查

答案： 【解析】：
人口普查是一项重大的国情国力调查，需要确保数据的全面性和准确性，以便为政府决策提供可靠依据。对于人口这样的关键数据，任何误差都可能影响到政策的制定和实施效果。
A选项指出“人口调查需要获得全面准确的信息”，这符合人口普查的目的和要求，因为全面准确的信息是制定有效政策的基础。
B选项提到“人口调查的数目不太大”，这与实际情况不符，因为全国人口普查涉及的人数是巨大的。
C选项中的“人口调查具有破坏性”显然不正确，因为人口调查不会对被调查者造成任何破坏或伤害。
D选项说“受条件限制，无法进行抽样调查”，这也不符合实际情况。虽然抽样调查在某些情况下是可行的，但全国人口普查需要的是全面数据，而不是样本数据。
因此，根据以上分析，A选项最符合全国人口普查采用普查方式的理由。
【答案】：A

1. 如图$10 - 3$所示,若直线$y = k x与四条直线x = 1$,$x = 2$,$y = 1$,$y = 2$围成的正方形有公共点,则$k$的取值范围是$\frac{1}{2}\leq k\leq2$.

答案： 【解析】：首先，确定四条直线$x = 1$，$x = 2$，$y = 1$，$y = 2$围成的正方形的四个顶点坐标。当$x = 1$，$y = 1$时，顶点为$(1,1)$；$x = 2$，$y = 1$时，顶点为$(2,1)$；$x = 2$，$y = 2$时，顶点为$(2,2)$；$x = 1$，$y = 2$时，顶点为$(1,2)$。
直线$y = kx$过原点$(0,0)$，要与该正方形有公共点，需考虑直线经过正方形边界或内部的情况。通过观察图形（图10-3左图），当直线$y = kx$经过正方形左下角顶点$(2,1)$时，斜率最小；经过右上角顶点$(1,2)$时，斜率最大。
将点$(2,1)$代入$y = kx$，可得$1 = 2k$，解得$k=\frac{1}{2}$；将点$(1,2)$代入$y = kx$，可得$2 = k×1$，解得$k = 2$。
因为直线$y = kx$的斜率$k$在$\frac{1}{2}$到$2$之间时，会与正方形有公共点，所以$k$的取值范围是$\frac{1}{2}\leq k\leq2$。
【答案】：$\frac{1}{2}\leq k\leq2$

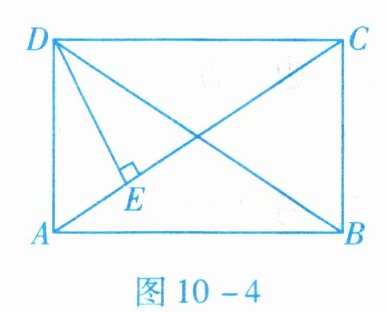
2. 如图$10 - 4$所示,在矩形$ABCD$中,$D E \perp A C于点E$,$E C = 3 A E$,$A D = 3 \mathrm{cm}$,那么$A C = $6.

答案： 【解析】：设 $ AE = x $，则 $ EC = 3x $，所以 $ AC = AE + EC = 4x $。
因为四边形 $ ABCD $ 是矩形，所以 $ \angle ADC = 90^\circ $，且 $ DE \perp AC $。根据直角三角形射影定理（在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项），可得 $ AD^2 = AE \cdot AC $。
已知 $ AD = 3\ \text{cm} $，代入可得：$ 3^2 = x \cdot 4x $，即 $ 9 = 4x^2 $，解得 $ x^2 = \frac{9}{4} $，$ x = \frac{3}{2} $（$ x ＞ 0 $）。
因此，$ AC = 4x = 4 × \frac{3}{2} = 6\ \text{cm} $。
【答案】：6

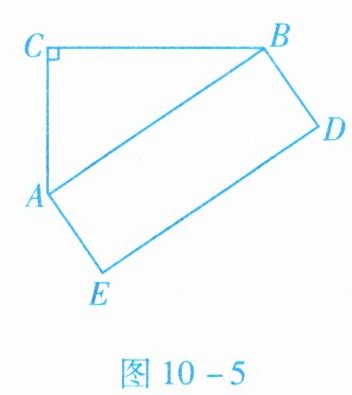
3. 如图$10 - 5$所示,已知$A C \perp B C$,$A C = 3$,$C B = 4$,$B D = 2$,则矩形$ABDE$的面积是____10.

答案： 【解析】：因为 $AC \perp BC$，所以$\triangle ABC$是直角三角形。根据勾股定理，$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+4^{2}} = 5$。由于四边形$ABDE$是矩形，所以它的面积等于$AB× BD$（这里$BD$是矩形的另一条边，题目中给出$BD = 2$）。因此，矩形$ABDE$的面积为$5×2=10$。
【答案】：10