《2025年暑假生活八年级数学河北少年儿童出版社》

1. 计算：$\sqrt {8}-\sqrt {18}= $$-\sqrt{2}$.

答案： 【解析】：
首先，我们需要将给定的根式化为最简形式。
对于 $\sqrt{8}$，我们可以将其分解为 $\sqrt{4 × 2} = 2\sqrt{2}$。
对于 $\sqrt{18}$，我们可以将其分解为 $\sqrt{9 × 2} = 3\sqrt{2}$。
然后，我们将这两个最简形式的根式进行相减：
$2\sqrt{2} - 3\sqrt{2} = -\sqrt{2}$
【答案】：$-\sqrt{2}$

2. 已知菱形$ ABCD $的周长为 40 cm,$∠ABC= 60^{\circ }$,则对角线$ BD $的长等于$10\sqrt{3}$cm.

答案： 【解析】：因为菱形$ABCD$的周长为$40\space cm$，菱形的四条边相等，所以每条边的长度为$40÷4 = 10\space cm$，即$AB=BC=CD=DA = 10\space cm$。
已知$\angle ABC=60^{\circ}$，在菱形中，相邻的边$AB = BC$，所以$\triangle ABC$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形），因此$AC=AB = 10\space cm$。
菱形的对角线互相垂直平分，设对角线$AC$与$BD$相交于点$O$，则$AO=\frac{1}{2}AC=\frac{1}{2}×10 = 5\space cm$，$BO=\frac{1}{2}BD$，且$\angle AOB = 90^{\circ}$。
在直角三角形$AOB$中，根据勾股定理$AB^{2}=AO^{2}+BO^{2}$，可得$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{10^{2}-5^{2}}=\sqrt{100 - 25}=\sqrt{75}=5\sqrt{3}\space cm$。
所以对角线$BD=2BO=2×5\sqrt{3}=10\sqrt{3}\space cm$。
【答案】：$10\sqrt{3}$

3. 若一次函数$y= kx+b的图象经过点(0,2)和(-2,0)$,则$ y 随 x $的增大而增大.(填“增大”或“减小”)

答案： 【解析】：
首先，我们使用给定的两点 $(0,2)$ 和 $(-2,0)$ 来确定一次函数的表达式。
将点 $(0,2)$ 代入 $y = kx + b$，得到：
$2 = k × 0 + b$
$b = 2$
再将点 $(-2,0)$ 代入 $y = kx + b$，得到：
$0 = k × (-2) + 2$
$-2k = -2$
$k = 1$
因此，一次函数的表达式为 $y = x + 2$。
由于斜率 $k = 1 ＞ 0$，根据一次函数的性质，当斜率大于0时，函数是增函数，即 $y$ 随 $x$ 的增大而增大。
【答案】：增大

4. 球的体积$V(cm^{3})与球的半径R(cm)之间的关系式是V= \frac {4}{3}πR^{3}$. 这里的常量是$\frac{4}{3}$，$\pi$.

答案： 【解析】：在球的体积与半径的关系式 $V = \frac{4}{3}\pi R^{3}$ 中，
$\frac{4}{3}$ 和 $\pi$ 都是不会改变的数值，而 $R$ 是可以变化的，代表球的半径。
因此，这里的常量是 $\frac{4}{3}$ 和 $\pi$。
【答案】：$\frac{4}{3}$，$\pi$

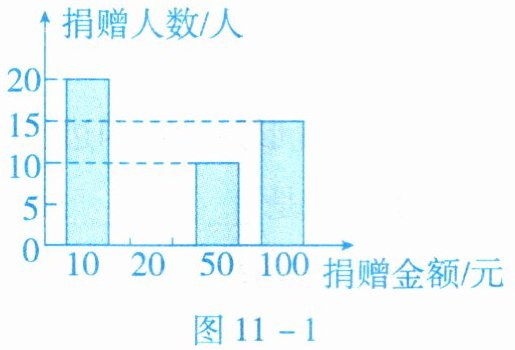
5. 在某次学校捐款活动中,把七年级捐款情况的统计结果绘制成如图 11 - 1 所示的不完整的统计图,其中七年级捐 10 元的人数占该年级捐款总人数的 25%,则七年级捐 20 元的人数为35人.

答案： 【解析】：
由图可知捐10元的有20人，
已知捐10元的人数占该年级捐款总人数的$25\%$，
所以七年级捐款总人数为$20÷25\%=20÷0.25 = 80$（人）。
从统计图中可知捐10元的有20人，捐50元的有10人，捐100元的有15人，
设捐20元的有$x$人，
根据总人数可列方程$20 + x + 10 + 15 = 80$，
即$x + 45 = 80$，
解得$x = 80 - 45 = 35$，
所以七年级捐20元的人数为35人。
【答案】：
35

1. 下列调查中,适合用普查的是(C)
A.了解某市学生的视力情况
B.了解某市中学生课外阅读的情况
C.了解某市百岁以上老人的健康情况
D.了解某市老年人参加晨练的情况

答案： 【解析】：
A. 了解某市学生的视力情况：由于学生数量可能较多，适合抽样调查，故A不适合普查；
B. 了解某市中学生课外阅读的情况：中学生数量众多，适合抽样调查，故B不适合普查；
C. 了解某市百岁以上老人的健康情况：百岁以上老人在一个市中的数量是相对较少的，因此可以对每一位都进行调查，适合普查，故C适合普查；
D. 了解某市老年人参加晨练的情况：老年人数量可能较多，适合抽样调查，故D不适合普查。
【答案】：C

2. 下列等式成立的是(D)
A.$2\sqrt {12}÷\sqrt {6}= 2$
B.$(\sqrt {2}+\sqrt {3})^{2}= 5+\sqrt {6}$
C.$(\sqrt {3}+\sqrt {5})(\sqrt {3}-\sqrt {5})= 2$
D.$3\sqrt {2}-\sqrt {2}= 2\sqrt {2}$

答案： 【解析】：
A. 对于 $2\sqrt{12} ÷ \sqrt{6}$，
我们可以先化简 $2\sqrt{12}$ 为 $4\sqrt{3}$，
然后除以 $\sqrt{6}$，
得到 $4\sqrt{3} ÷ \sqrt{6} = 2\sqrt{2}$，
与选项A给出的 $2$ 不符，
所以A选项错误。
B. 对于 $(\sqrt{2} + \sqrt{3})^{2}$，
使用平方差公式展开得到：
$(\sqrt{2} + \sqrt{3})^{2} = 2 + 2\sqrt{6} + 3 = 5 + 2\sqrt{6}$
与选项B给出的 $5 + \sqrt{6}$ 不符，
所以B选项错误。
C. 对于 $(\sqrt{3} + \sqrt{5})(\sqrt{3} - \sqrt{5})$，
使用平方差公式得到：
$(\sqrt{3} + \sqrt{5})(\sqrt{3} - \sqrt{5}) = 3 - 5 = -2$
与选项C给出的 $2$ 不符，
所以C选项错误。
D. 对于 $3\sqrt{2} - \sqrt{2}$，
直接进行减法运算得到 $2\sqrt{2}$，
与选项D给出的 $2\sqrt{2}$ 相符，
所以D选项正确。
【答案】：D