2025年暑假生活八年级数学河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活八年级数学河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 请写出一个图象经过第一、三象限的正比例函数的表达式
$y=x$(答案不唯一,只要$k>0$即可)
.
答案:
【解析】:
正比例函数的一般形式为 $y = kx$,其中 $k$ 是比例系数。
由于图象需要经过第一、三象限,根据正比例函数的性质,当 $k > 0$ 时,图象会经过第一、三象限。
因此,可以选择 $k = 1$(或其他任何正数)来构造满足条件的正比例函数。
【答案】:$y = x$(答案不唯一,如 $y = 2x, y = 3x$ 等均可)
正比例函数的一般形式为 $y = kx$,其中 $k$ 是比例系数。
由于图象需要经过第一、三象限,根据正比例函数的性质,当 $k > 0$ 时,图象会经过第一、三象限。
因此,可以选择 $k = 1$(或其他任何正数)来构造满足条件的正比例函数。
【答案】:$y = x$(答案不唯一,如 $y = 2x, y = 3x$ 等均可)
2. 若式子$\frac {x}{x+1}-\sqrt {1-2x}$在实数范围内有意义,则$x$的取值范围为
$x\leq\frac{1}{2}$且$x\neq - 1$
.
答案:
【解析】:
要使式子$\frac {x}{x+1}-\sqrt {1-2x}$在实数范围内有意义,需要满足以下两个条件:
分式的分母不能为0,即$x+1 \neq 0$,解得$x \neq -1$。
二次根式下的表达式非负,即$1-2x \geq 0$,移项得$2x \leq 1$,进一步解得$x \leq \frac{1}{2}$。
综合以上两个条件,得到$x$的取值范围为$x \leq \frac{1}{2}$且$x \neq -1$。
【答案】:$x \leq \frac{1}{2}$且$x \neq -1$。
要使式子$\frac {x}{x+1}-\sqrt {1-2x}$在实数范围内有意义,需要满足以下两个条件:
分式的分母不能为0,即$x+1 \neq 0$,解得$x \neq -1$。
二次根式下的表达式非负,即$1-2x \geq 0$,移项得$2x \leq 1$,进一步解得$x \leq \frac{1}{2}$。
综合以上两个条件,得到$x$的取值范围为$x \leq \frac{1}{2}$且$x \neq -1$。
【答案】:$x \leq \frac{1}{2}$且$x \neq -1$。
3. 将正比例函数$y= -6x$的图象向上平移,那么平移后所得图象对应的函数表达式可能是
$y = -6x + 1$
.(填一个即可)
答案:
【解析】:
对于正比例函数$y = -6x$,其图象是一条经过原点的直线。当这条直线向上平移时,每一个点的$y$坐标都会增加一个固定的值,而$x$坐标保持不变。因此,平移后的函数表达式可以表示为$y = -6x + b$,其中$b$是一个大于$0$的常数,表示向上平移的距离。
为了得到一个可能的答案,我们可以选择$b$为任意正数,例如$b = 9$,那么平移后所得图象对应的函数表达式就是$y = -6x + 9$。
【答案】:
$y = - 6x + 9$(答案不唯一)
对于正比例函数$y = -6x$,其图象是一条经过原点的直线。当这条直线向上平移时,每一个点的$y$坐标都会增加一个固定的值,而$x$坐标保持不变。因此,平移后的函数表达式可以表示为$y = -6x + b$,其中$b$是一个大于$0$的常数,表示向上平移的距离。
为了得到一个可能的答案,我们可以选择$b$为任意正数,例如$b = 9$,那么平移后所得图象对应的函数表达式就是$y = -6x + 9$。
【答案】:
$y = - 6x + 9$(答案不唯一)
4. 某学校为了做好道路交通安全教育工作,随机抽取了本校100名学生就上学的交通方式进行调查,根据调查结果绘制出了如图8-1所示的扇形统计图. 若该校共有1000名学生,则估计全校步行上学的学生约有
400
名.
答案:
【解析】:从扇形统计图中可知,步行上学的学生所占比例为:
$1 - 25\% - 25\% - 10\% = 40\%$。
已知该校共有$1000$名学生,那么全校步行上学的学生人数约为:
$1000× 40\% = 1000× 0.4 = 400$(名)。
【答案】:400
$1 - 25\% - 25\% - 10\% = 40\%$。
已知该校共有$1000$名学生,那么全校步行上学的学生人数约为:
$1000× 40\% = 1000× 0.4 = 400$(名)。
【答案】:400
5. 计算:$\sqrt {96}+\sqrt {150}=$
$9\sqrt{6}$
.
答案:
【解析】:先将根号下的数分解因数,化为最简二次根式。
$\sqrt{96} = \sqrt{16 × 6} = \sqrt{16} × \sqrt{6} = 4\sqrt{6}$
$\sqrt{150} = \sqrt{25 × 6} = \sqrt{25} × \sqrt{6} = 5\sqrt{6}$
然后将同类二次根式相加:$4\sqrt{6} + 5\sqrt{6} = (4 + 5)\sqrt{6} = 9\sqrt{6}$
【答案】:$9\sqrt{6}$
$\sqrt{96} = \sqrt{16 × 6} = \sqrt{16} × \sqrt{6} = 4\sqrt{6}$
$\sqrt{150} = \sqrt{25 × 6} = \sqrt{25} × \sqrt{6} = 5\sqrt{6}$
然后将同类二次根式相加:$4\sqrt{6} + 5\sqrt{6} = (4 + 5)\sqrt{6} = 9\sqrt{6}$
【答案】:$9\sqrt{6}$
1. 已知$□ ABCD$中,$∠A+∠C= 200^{\circ }$,则$∠B$的度数是(
A.$100^{\circ }$
B.$160^{\circ }$
C.$80^{\circ }$
D.$60^{\circ }$
C
)A.$100^{\circ }$
B.$160^{\circ }$
C.$80^{\circ }$
D.$60^{\circ }$
答案:
【解析】:
在平行四边形$ABCD$中,由于$AD // BC$,根据平行线的性质,我们有$\angle A + \angle B = 180^{\circ}$(同旁内角互补)。
又因为题目给出$\angle A + \angle C = 200^{\circ}$,并且在平行四边形中,$\angle A = \angle C$(对角相等),我们可以求出$\angle A$和$\angle C$的具体度数:
$\angle A = \angle C = \frac{200^{\circ}}{2} = 100^{\circ}$
然后,利用$\angle A + \angle B = 180^{\circ}$求出$\angle B$:
$\angle B = 180^{\circ} - \angle A = 180^{\circ} - 100^{\circ} = 80^{\circ}$
【答案】:C.$80^{\circ}$
在平行四边形$ABCD$中,由于$AD // BC$,根据平行线的性质,我们有$\angle A + \angle B = 180^{\circ}$(同旁内角互补)。
又因为题目给出$\angle A + \angle C = 200^{\circ}$,并且在平行四边形中,$\angle A = \angle C$(对角相等),我们可以求出$\angle A$和$\angle C$的具体度数:
$\angle A = \angle C = \frac{200^{\circ}}{2} = 100^{\circ}$
然后,利用$\angle A + \angle B = 180^{\circ}$求出$\angle B$:
$\angle B = 180^{\circ} - \angle A = 180^{\circ} - 100^{\circ} = 80^{\circ}$
【答案】:C.$80^{\circ}$
2. 空气是由多种气体混合而成的,为了简明扼要地介绍空气的组成情况,较好地描述数据,最适合使用的统计图是(
A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
A
)A.扇形统计图
B.条形统计图
C.折线统计图
D.频数分布直方图
答案:
【解析】:
扇形统计图:主要用于表示各部分在总体中所占的比例,能够清晰地展示各部分与总体的关系。
条形统计图:主要用于表示不同类别的数据大小,便于比较各类别之间的差异。
折线统计图:主要用于表示数据随时间或其他连续变量的变化趋势。
频数分布直方图:主要用于表示数据的分布情况,特别是连续变量的频数分布。
在本题中,目的是要简明扼要地介绍空气的组成情况,即要展示空气中各气体成分所占的比例。因此,扇形统计图是最适合的,因为它能够清晰地展示各部分在总体中的比例。
【答案】:A
扇形统计图:主要用于表示各部分在总体中所占的比例,能够清晰地展示各部分与总体的关系。
条形统计图:主要用于表示不同类别的数据大小,便于比较各类别之间的差异。
折线统计图:主要用于表示数据随时间或其他连续变量的变化趋势。
频数分布直方图:主要用于表示数据的分布情况,特别是连续变量的频数分布。
在本题中,目的是要简明扼要地介绍空气的组成情况,即要展示空气中各气体成分所占的比例。因此,扇形统计图是最适合的,因为它能够清晰地展示各部分在总体中的比例。
【答案】:A
3. 若式子$\sqrt {3x-4}$在实数范围内有意义,则$x$的取值范围是(
A.$x≥\frac {4}{3}$
B.$x>\frac {4}{3}$
C.$x≥\frac {3}{4}$
D.$x>\frac {3}{4}$
A
)A.$x≥\frac {4}{3}$
B.$x>\frac {4}{3}$
C.$x≥\frac {3}{4}$
D.$x>\frac {3}{4}$
答案:
【解析】:要使二次根式$\sqrt{3x - 4}$在实数范围内有意义,被开方数必须是非负数,即$3x - 4 \geq 0$。解这个不等式:$3x \geq 4$,两边同时除以$3$,得到$x \geq \frac{4}{3}$。
【答案】:A
【答案】:A
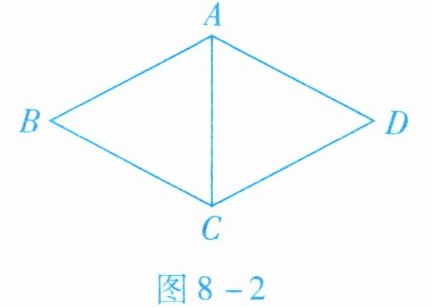
4. 如图8-2所示,在菱形$ABCD$中,$AB= 5$,$∠BCD= 120^{\circ }$,则$\triangle ABC$的周长是(
A.20
B.15
C.10
D.5
B
)
A.20
B.15
C.10
D.5
答案:
【解析】:在菱形$ABCD$中,$AB = BC = CD = DA = 5$(菱形的四条边相等)。因为$\angle BCD = 120^{\circ}$,菱形的邻角互补,所以$\angle ABC = 180^{\circ}-\angle BCD=180^{\circ}-120^{\circ} = 60^{\circ}$。在$\triangle ABC$中,$AB = BC = 5$,且$\angle ABC = 60^{\circ}$,所以$\triangle ABC$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形),因此$AC = AB = BC = 5$。则$\triangle ABC$的周长为$AB + BC + AC=5 + 5 + 5=15$。
【答案】:B
【答案】:B
查看更多完整答案,请扫码查看


