2025年暑假生活八年级数学河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活八年级数学河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列各式$y= 2x$,$y= \frac {1}{x}$,$y= |x|-1$,$|y|= x$,$y= x^{2}$中,$y是x$的函数的个数为(
A.5
B.4
C.3
D.2
B
)A.5
B.4
C.3
D.2
答案:
【解析】:根据函数的定义,对于x的每一个确定的值,y都有唯一确定的值与之对应。
$y=2x$:对于任意x,y都有唯一确定的值,是函数。
$y=\frac{1}{x}$:x≠0时,y有唯一确定的值,是函数。
$y=|x|-1$:对于任意x,y都有唯一确定的值,是函数。
$|y|=x$:当x>0时,y有两个值(正负)与之对应,不满足唯一性,不是函数。
$y=x^2$:对于任意x,y都有唯一确定的值,是函数。
综上,是函数的有4个。
【答案】:B
$y=2x$:对于任意x,y都有唯一确定的值,是函数。
$y=\frac{1}{x}$:x≠0时,y有唯一确定的值,是函数。
$y=|x|-1$:对于任意x,y都有唯一确定的值,是函数。
$|y|=x$:当x>0时,y有两个值(正负)与之对应,不满足唯一性,不是函数。
$y=x^2$:对于任意x,y都有唯一确定的值,是函数。
综上,是函数的有4个。
【答案】:B
2. 已知一次函数$y= kx+b$的图象经过第一、二、四象限,且与$x轴交于点(2,0)$,则关于$x的不等式k(x-1)-b>0$的解集为(
A.$x<-1$
B.$x>-1$
C.$x>1$
D.$x<1$
A
)A.$x<-1$
B.$x>-1$
C.$x>1$
D.$x<1$
答案:
【解析】:已知一次函数$y = kx + b$的图象经过第一、二、四象限,根据一次函数的性质可知,$k < 0$(斜率为负,函数从左到右下降),$b > 0$(与$y$轴交点在正半轴)。
因为函数与$x$轴交于点$(2, 0)$,将$x = 2$,$y = 0$代入$y = kx + b$,可得$0 = 2k + b$,即$b=-2k$。
接下来解不等式$k(x - 1)-b > 0$,将$b = -2k$代入不等式中,得到:
$\begin{aligned}k(x - 1)-(-2k)&>0\\k(x - 1)+2k&>0\\k[(x - 1)+2]&>0\\k(x + 1)&>0\end{aligned}$
由于$k < 0$,不等式两边同时除以一个负数,不等号方向改变,所以:
$x + 1 < 0$
解得$x < -1$。
【答案】:A
因为函数与$x$轴交于点$(2, 0)$,将$x = 2$,$y = 0$代入$y = kx + b$,可得$0 = 2k + b$,即$b=-2k$。
接下来解不等式$k(x - 1)-b > 0$,将$b = -2k$代入不等式中,得到:
$\begin{aligned}k(x - 1)-(-2k)&>0\\k(x - 1)+2k&>0\\k[(x - 1)+2]&>0\\k(x + 1)&>0\end{aligned}$
由于$k < 0$,不等式两边同时除以一个负数,不等号方向改变,所以:
$x + 1 < 0$
解得$x < -1$。
【答案】:A
3. 从等腰三角形底边上任意一点,分别作两腰的平行线,那么所形成的平行四边形的周长等于这个等腰三角形的(
A.周长的一半
B.周长
C.两腰长之和
D.腰长
C
)A.周长的一半
B.周长
C.两腰长之和
D.腰长
答案:
【解析】:设等腰三角形为$△ABC$,$AB = AC$,底边$BC$上任意一点为$D$,过$D$作$DE// AC$交$AB$于$E$,作$DF// AB$交$AC$于$F$,则四边形$AEDF$是平行四边形,所以$DE = AF$,$DF = AE$,平行四边形$AEDF$的周长为$2(AE + AF)$。
因为$DE// AC$,所以$\angle EDB=\angle C$,又因为$AB = AC$,所以$\angle B=\angle C$,故$\angle EDB=\angle B$,则$EB = ED$,同理$FD = FC$。
所以$AE + EB = AB$,即$AE + ED = AB$,而$ED = AF$,所以$AE + AF = AB$,因此平行四边形$AEDF$的周长为$2AB$,即等于等腰三角形两腰长之和。
【答案】:C
因为$DE// AC$,所以$\angle EDB=\angle C$,又因为$AB = AC$,所以$\angle B=\angle C$,故$\angle EDB=\angle B$,则$EB = ED$,同理$FD = FC$。
所以$AE + EB = AB$,即$AE + ED = AB$,而$ED = AF$,所以$AE + AF = AB$,因此平行四边形$AEDF$的周长为$2AB$,即等于等腰三角形两腰长之和。
【答案】:C
4. 如图8-7所示,在边长为2的正方形$ABCD$中,$M为边AD$的中点,延长$MD至点E$,使$ME= MC$,以$DE为边作正方形DEFG$,点$G在边CD$上,则$DG$的长为(

A.$\sqrt {3}-1$
B.$3-\sqrt {5}$
C.$\sqrt {5}+1$
D.$\sqrt {5}-1$
D
)
A.$\sqrt {3}-1$
B.$3-\sqrt {5}$
C.$\sqrt {5}+1$
D.$\sqrt {5}-1$
答案:
【解析】:在正方形$ABCD$中,边长为$2$,$M$为$AD$中点,所以$AM = MD=1$,$CD = 2$。在$Rt\triangle MCD$中,根据勾股定理可得$MC=\sqrt{MD^{2}+CD^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$。因为$ME = MC$,所以$ME=\sqrt{5}$,又因为$MD = 1$,所以$DE=ME - MD=\sqrt{5}-1$。由于四边形$DEFG$是正方形,所以$DG = DE=\sqrt{5}-1$。
【答案】:D
【答案】:D
5. 如图8-8①所示,$□ ABCD$中,$AD>AB$,$∠ABC$为锐角. 要在对角线$BD上找点N$,$M$,使四边形$ANCM$为平行四边形,现有图8-8②中的甲、乙、丙三种方案,则正确的方案(
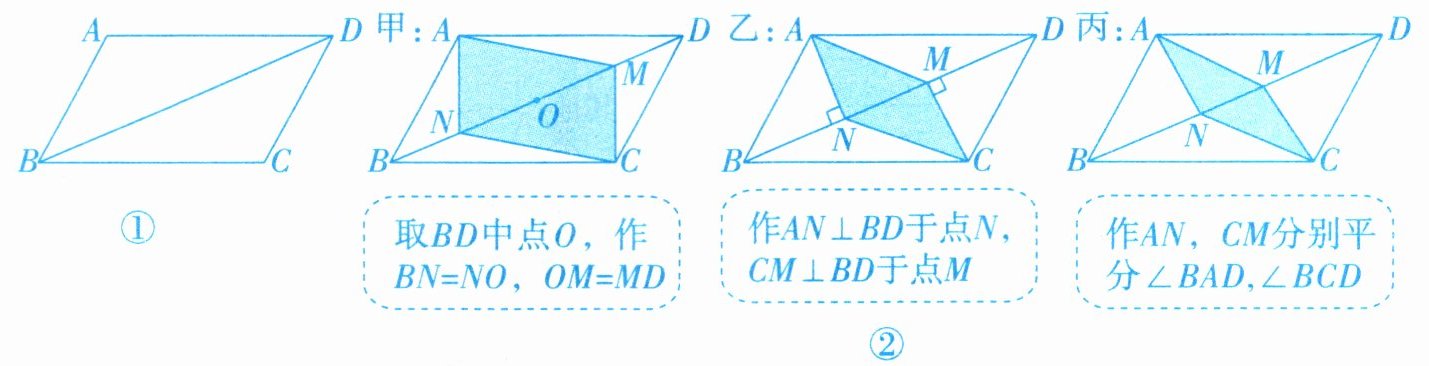
A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是
D.只有乙、丙才是
A
)
A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是
D.只有乙、丙才是
答案:
【解析】:在平行四边形$ABCD$中,$AB// CD$,$AB = CD$,$\angle ABD=\angle CDB$,$AD// BC$,$AD = BC$,$\angle ADB=\angle CBD$。
甲方案:取$BD$中点$O$,$BN = NO$,$OM=MD$。
因为$O$是$BD$中点,所以$BO = OD$。
由$BN=NO$可得$NO=\frac{1}{2}BO$,由$OM = MD$可得$OM=\frac{1}{2}OD$,又因为$BO = OD$,所以$NO=OM$。
因为$BO = OD$,$BN=NO$,所以$BN + NO=BO$,即$2NO=BO$,同理$2OM=OD$,所以$NO = OM$,则$BN=NO=OM=MD$,所以$BN + NO=OM + MD$,即$BN + NO=OD$,又因为$BO = OD$,所以$BN + NO=BO$,即$N$为$BO$中点,$M$为$OD$中点,所以$ON=OM$。
在四边形$ANCM$中,对角线$AC$与$NM$相交于点$O$,$AO = OC$(平行四边形对角线互相平分),$NO=OM$,所以四边形$ANCM$是平行四边形(对角线互相平分的四边形是平行四边形),甲方案正确。
乙方案:作$AN\perp BD$于$N$,$CM\perp BD$于$M$。
因为$AN\perp BD$,$CM\perp BD$,所以$\angle ANO=\angle CMO = 90^{\circ}$(设$AC$与$BD$交于点$O$)。
在平行四边形$ABCD$中,$AO = OC$,$\angle AON=\angle COM$(对顶角相等)。
在$\triangle ANO$和$\triangle CMO$中,$\left\{\begin{array}{l}\angle ANO=\angle CMO\\\angle AON=\angle COM\\AO = CO\end{array}\right.$,所以$\triangle ANO\cong\triangle CMO(AAS)$,则$AN = CM$,$ON=OM$。
因为$AN\perp BD$,$CM\perp BD$,所以$AN// CM$(垂直于同一条直线的两条直线平行),又因为$AN = CM$,所以四边形$ANCM$是平行四边形(一组对边平行且相等的四边形是平行四边形),乙方案正确。
丙方案:作$AN$平分$\angle BAD$,$CM$平分$\angle BCD$。
在平行四边形$ABCD$中,$\angle BAD=\angle BCD$(平行四边形对角相等),因为$AN$平分$\angle BAD$,$CM$平分$\angle BCD$,所以$\angle BAN=\angle DAN=\frac{1}{2}\angle BAD$,$\angle BCM=\angle DCM=\frac{1}{2}\angle BCD$,所以$\angle BAN=\angle DCM$,$\angle DAN=\angle BCM$。
因为$AD// BC$,所以$\angle ADB=\angle CBD$。
在$\triangle ADN$和$\triangle CBM$中,$\angle DAN=\angle BCM$,$AD = BC$(平行四边形对边相等),$\angle ADN=\angle CBM$,所以$\triangle ADN\cong\triangle CBM(ASA)$,则$AN = CM$,$DN = BM$。
因为$BD = BD$,$DN=BM$,所以$BD - DN=BD - BM$,即$BN = DM$。
在$\triangle ABN$和$\triangle CDM$中,$AB = CD$(平行四边形对边相等),$\angle ABN=\angle CDM$(平行四边形对边平行,内错角相等),$BN = DM$,所以$\triangle ABN\cong\triangle CDM(SAS)$,则$\angle ANB=\angle CMD$,所以$\angle ANM=\angle CMN$(等角的补角相等),所以$AN// CM$。
因为$AN = CM$且$AN// CM$,所以四边形$ANCM$是平行四边形(一组对边平行且相等的四边形是平行四边形),丙方案正确。
综上,甲、乙、丙三种方案都正确。
【答案】:A
甲方案:取$BD$中点$O$,$BN = NO$,$OM=MD$。
因为$O$是$BD$中点,所以$BO = OD$。
由$BN=NO$可得$NO=\frac{1}{2}BO$,由$OM = MD$可得$OM=\frac{1}{2}OD$,又因为$BO = OD$,所以$NO=OM$。
因为$BO = OD$,$BN=NO$,所以$BN + NO=BO$,即$2NO=BO$,同理$2OM=OD$,所以$NO = OM$,则$BN=NO=OM=MD$,所以$BN + NO=OM + MD$,即$BN + NO=OD$,又因为$BO = OD$,所以$BN + NO=BO$,即$N$为$BO$中点,$M$为$OD$中点,所以$ON=OM$。
在四边形$ANCM$中,对角线$AC$与$NM$相交于点$O$,$AO = OC$(平行四边形对角线互相平分),$NO=OM$,所以四边形$ANCM$是平行四边形(对角线互相平分的四边形是平行四边形),甲方案正确。
乙方案:作$AN\perp BD$于$N$,$CM\perp BD$于$M$。
因为$AN\perp BD$,$CM\perp BD$,所以$\angle ANO=\angle CMO = 90^{\circ}$(设$AC$与$BD$交于点$O$)。
在平行四边形$ABCD$中,$AO = OC$,$\angle AON=\angle COM$(对顶角相等)。
在$\triangle ANO$和$\triangle CMO$中,$\left\{\begin{array}{l}\angle ANO=\angle CMO\\\angle AON=\angle COM\\AO = CO\end{array}\right.$,所以$\triangle ANO\cong\triangle CMO(AAS)$,则$AN = CM$,$ON=OM$。
因为$AN\perp BD$,$CM\perp BD$,所以$AN// CM$(垂直于同一条直线的两条直线平行),又因为$AN = CM$,所以四边形$ANCM$是平行四边形(一组对边平行且相等的四边形是平行四边形),乙方案正确。
丙方案:作$AN$平分$\angle BAD$,$CM$平分$\angle BCD$。
在平行四边形$ABCD$中,$\angle BAD=\angle BCD$(平行四边形对角相等),因为$AN$平分$\angle BAD$,$CM$平分$\angle BCD$,所以$\angle BAN=\angle DAN=\frac{1}{2}\angle BAD$,$\angle BCM=\angle DCM=\frac{1}{2}\angle BCD$,所以$\angle BAN=\angle DCM$,$\angle DAN=\angle BCM$。
因为$AD// BC$,所以$\angle ADB=\angle CBD$。
在$\triangle ADN$和$\triangle CBM$中,$\angle DAN=\angle BCM$,$AD = BC$(平行四边形对边相等),$\angle ADN=\angle CBM$,所以$\triangle ADN\cong\triangle CBM(ASA)$,则$AN = CM$,$DN = BM$。
因为$BD = BD$,$DN=BM$,所以$BD - DN=BD - BM$,即$BN = DM$。
在$\triangle ABN$和$\triangle CDM$中,$AB = CD$(平行四边形对边相等),$\angle ABN=\angle CDM$(平行四边形对边平行,内错角相等),$BN = DM$,所以$\triangle ABN\cong\triangle CDM(SAS)$,则$\angle ANB=\angle CMD$,所以$\angle ANM=\angle CMN$(等角的补角相等),所以$AN// CM$。
因为$AN = CM$且$AN// CM$,所以四边形$ANCM$是平行四边形(一组对边平行且相等的四边形是平行四边形),丙方案正确。
综上,甲、乙、丙三种方案都正确。
【答案】:A
查看更多完整答案,请扫码查看


