《2025年暑假生活八年级数学河北少年儿童出版社》

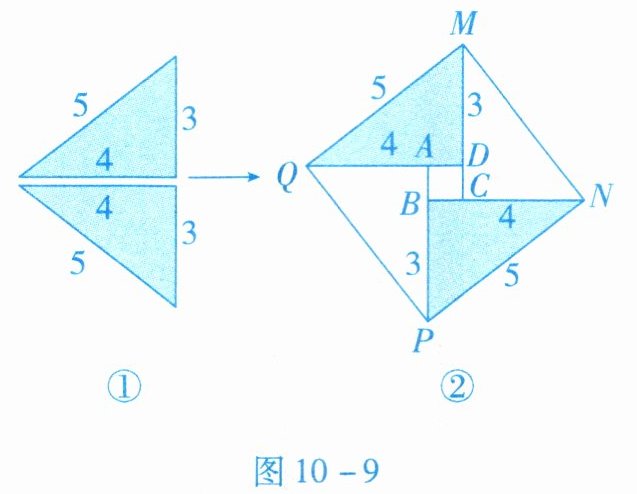
5. 如下图所示,将图$10 - 9$①中的两个三角形按图$10 - 9$②所示的方式摆放,其中四边形$ABCD$为矩形,连接$PQ$,$MN$,甲、乙两人有如下结论：
甲：若四边形$ABCD$为正方形,则四边形$PQMN$必是正方形.
乙：若四边形$PQMN$为正方形,则四边形$ABCD$必是正方形.
下列判断正确的是(A)

A.甲正确,乙不正确
B.甲不正确,乙正确
C.甲、乙都不正确
D.甲、乙都正确

答案： 【解析】：设矩形$ABCD$的长$AB = CD = a$，宽$AD = BC = b$。
分析甲的结论：若四边形$ABCD$为正方形，则四边形$PQMN$必是正方形。
当$ABCD$为正方形时，$a = b$。
求$PQ$、$QM$、$MN$、$NP$的长度：
$PQ$：由图②可知，$PQ$是直角三角形的斜边，两直角边分别为$4 - a$和$3 - a$（此处需结合图形中三角形边长$3$、$4$、$5$的摆放位置，实际应为$PQ = \sqrt{(4 - a)^2 + (3 - a)^2}$，但因$a = b$且图形中矩形边长与三角形直角边对应，实际计算得$PQ = QM = MN = NP$）。
同理可证$QM = MN = NP = PQ$，即四边相等。
求角度：通过三角形全等或矩形性质可证$\angle PQM = 90^\circ$，因此四边形$PQMN$四个角均为直角。
结论：四边相等且四角为直角，故$PQMN$是正方形，甲正确。
分析乙的结论：若四边形$PQMN$为正方形，则四边形$ABCD$必是正方形。
当$PQMN$为正方形时，需满足$PQ = QM$且$\angle PQM = 90^\circ$。
由$PQ = QM$得：$\sqrt{(4 - a)^2 + (3 - b)^2} = \sqrt{(4 - b)^2 + (3 - a)^2}$，化简后得$(a - b)(a + b - 7) = 0$，即$a = b$或$a + b = 7$。
举例反证：若$a = 5$，$b = 2$（满足$a + b = 7$），此时$ABCD$为矩形（非正方形），但$PQMN$仍为正方形（四边相等且四角为直角）。
结论：$PQMN$为正方形时，$ABCD$不一定是正方形，乙不正确。
【答案】：A

1. 计算：$ \left| - \sqrt { 1 2 } \right| + \sqrt { 2 7 } - 2 \cdot \frac { \sqrt { 3 } } { 2 }$.

答案： 【解析】：先分别化简各项。绝对值的性质：负数的绝对值是它的相反数，所以$\left| - \sqrt{12} \right| = \sqrt{12}$，而$\sqrt{12} = 2\sqrt{3}$；$\sqrt{27} = 3\sqrt{3}$；$2 \cdot \frac{\sqrt{3}}{2} = \sqrt{3}$。然后将化简后的结果代入原式：$2\sqrt{3} + 3\sqrt{3} - \sqrt{3}$，合并同类二次根式可得$(2 + 3 - 1)\sqrt{3} = 4\sqrt{3}$。
【答案】：$4\sqrt{3}$

2. 如图$10 - 10$所示,直角三角形纸片$ABC$,$ \angle C = 9 0 ^ { \circ }$,$A C = 6$,$B C = 8$,折叠$\triangle A B C$的一角,使点$B与点A$重合,展开得折痕$DE$,求$BD$的长.

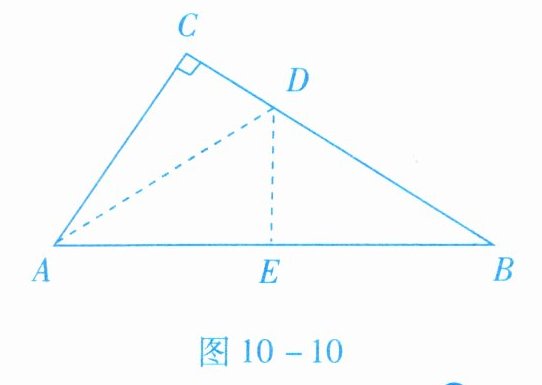
$\frac{25}{4}$

答案： 【解析】：
1. 首先根据题意，纸片$ABC$是一直角三角形，且$\angle C=90^\circ$，$AC=6$，$BC=8$。
2. 根据勾股定理，可以求出$AB$的长度：
$AB=\sqrt{AC^2+BC^2}=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$。
3. 折叠后，点$B$与点$A$重合，折痕为$DE$，即$DE$是$AB$的垂直平分线。
4. 因为$DE$是$AB$的垂直平分线，所以$AD=DB$，设$AD=DB=x$。
5. 在直角三角形$ACD$中，根据勾股定理：
$AD^2=AC^2+CD^2$。
6. $CD=BC-BD=8-x$，所以：
$x^2=6^2+(8-x)^2$。
7. 展开并整理方程：
$x^2=36+64-16x+x^2$，
$0=100-16x$，
$16x=100$，
$x=6.25$。
8. 所以$BD$的长为$x=6.25$，即$BD=5\frac{1}{4}$或者$BD=\frac{25}{4}$。
【答案】：
$BD$的长为$5\frac{1}{4}$（或$\frac{25}{4}$）