2025年暑假生活八年级数学河北少年儿童出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活八年级数学河北少年儿童出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
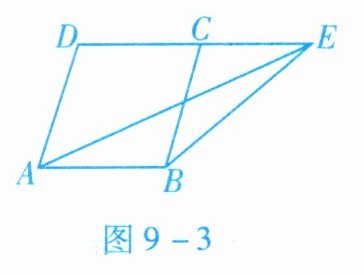
3. 如图9-3所示,$E是□ ABCD的边DC$延长线上一点,且$S_{□ ABCD}= 16cm^{2}$,则$S_{\triangle ABE}= $(
A.$8cm^{2}$
B.$16cm^{2}$
C.$24cm^{2}$
D.$32cm^{2}$
A
)
A.$8cm^{2}$
B.$16cm^{2}$
C.$24cm^{2}$
D.$32cm^{2}$
答案:
【解析】:在平行四边形 $ABCD$ 中,$AB // DC$,且 $AB = DC$。点 $E$ 在 $DC$ 的延长线上,所以 $AB // DE$。
由于 $AB$ 和 $DE$ 平行,$\triangle ABE$ 与平行四边形 $ABCD$ 同底($AB$)且等高(平行线 $AB$ 与 $DE$ 之间的距离)。
平行四边形的面积公式为 $S = 底 × 高$,即 $S_{□ ABCD} = AB × h = 16\ \text{cm}^2$(其中 $h$ 为 $AB$ 与 $DC$ 之间的距离)。
$\triangle ABE$ 的面积公式为 $S = \frac{1}{2} × 底 × 高$,这里底为 $AB$,高与平行四边形的高 $h$ 相等,因此 $S_{\triangle ABE} = \frac{1}{2} × AB × h = \frac{1}{2} × S_{□ ABCD} = \frac{1}{2} × 16 = 8\ \text{cm}^2$。
【答案】:A
由于 $AB$ 和 $DE$ 平行,$\triangle ABE$ 与平行四边形 $ABCD$ 同底($AB$)且等高(平行线 $AB$ 与 $DE$ 之间的距离)。
平行四边形的面积公式为 $S = 底 × 高$,即 $S_{□ ABCD} = AB × h = 16\ \text{cm}^2$(其中 $h$ 为 $AB$ 与 $DC$ 之间的距离)。
$\triangle ABE$ 的面积公式为 $S = \frac{1}{2} × 底 × 高$,这里底为 $AB$,高与平行四边形的高 $h$ 相等,因此 $S_{\triangle ABE} = \frac{1}{2} × AB × h = \frac{1}{2} × S_{□ ABCD} = \frac{1}{2} × 16 = 8\ \text{cm}^2$。
【答案】:A
4. 计算$(3\sqrt {5}-2\sqrt {7})(3\sqrt {5}+2\sqrt {7})$的值是(
A.15
B.16
C.17
D.18
C
)A.15
B.16
C.17
D.18
答案:
【解析】:
根据平方差公式$(a-b)(a+b)=a^{2}-b^{2}$,
将$a = 3\sqrt{5}$,$b = 2\sqrt{7}$代入可得:
$(3\sqrt{5}-2\sqrt{7})(3\sqrt{5}+2\sqrt{7})=(3\sqrt{5})^{2}-(2\sqrt{7})^{2}$
根据根式的平方运算规则$(\sqrt{a})^{2}=a$($a\geq0$),可得:
$(3\sqrt{5})^{2}=3^{2}×(\sqrt{5})^{2}=9×5 = 45$
$(2\sqrt{7})^{2}=2^{2}×(\sqrt{7})^{2}=4×7 = 28$
则$(3\sqrt{5})^{2}-(2\sqrt{7})^{2}=45 - 28 = 17$。
【答案】:C
根据平方差公式$(a-b)(a+b)=a^{2}-b^{2}$,
将$a = 3\sqrt{5}$,$b = 2\sqrt{7}$代入可得:
$(3\sqrt{5}-2\sqrt{7})(3\sqrt{5}+2\sqrt{7})=(3\sqrt{5})^{2}-(2\sqrt{7})^{2}$
根据根式的平方运算规则$(\sqrt{a})^{2}=a$($a\geq0$),可得:
$(3\sqrt{5})^{2}=3^{2}×(\sqrt{5})^{2}=9×5 = 45$
$(2\sqrt{7})^{2}=2^{2}×(\sqrt{7})^{2}=4×7 = 28$
则$(3\sqrt{5})^{2}-(2\sqrt{7})^{2}=45 - 28 = 17$。
【答案】:C
5. 下列式子:①$y= 3x-5$;②$y= \frac {1}{x}$;③$y= \sqrt {x-1}$;④$y^{2}= x$;⑤$y= |x|$.其中$y是x$的函数的个数是(
A.2
B.3
C.4
D.5
C
)A.2
B.3
C.4
D.5
答案:
【解析】:
对于给出的五个式子,我们需要逐一判断其是否满足函数的定义,即对于每一个$x$,$y$是否有唯一的值与之对应。
① $y = 3x - 5$:这是一个线性函数,对于每一个$x$,$y$都有唯一的值,所以它是函数。
② $y = \frac{1}{x}$:对于每一个非零的$x$,$y$都有唯一的值,所以它也是函数。
③ $y = \sqrt{x - 1}$:对于每一个$x \geq 1$,$y$都有唯一的值(非负数),所以它也是函数。
④ $y^2 = x$:例如,当$x = 4$时,$y$可以是$2$或$-2$,即对于同一个$x$,$y$有两个可能的值,所以它不是函数。
⑤ $y = |x|$:对于每一个$x$,$y$都有唯一的值($x$的绝对值),所以它是函数。
综上所述,是函数的式子有①、②、③、⑤,共4个。
【答案】:C
对于给出的五个式子,我们需要逐一判断其是否满足函数的定义,即对于每一个$x$,$y$是否有唯一的值与之对应。
① $y = 3x - 5$:这是一个线性函数,对于每一个$x$,$y$都有唯一的值,所以它是函数。
② $y = \frac{1}{x}$:对于每一个非零的$x$,$y$都有唯一的值,所以它也是函数。
③ $y = \sqrt{x - 1}$:对于每一个$x \geq 1$,$y$都有唯一的值(非负数),所以它也是函数。
④ $y^2 = x$:例如,当$x = 4$时,$y$可以是$2$或$-2$,即对于同一个$x$,$y$有两个可能的值,所以它不是函数。
⑤ $y = |x|$:对于每一个$x$,$y$都有唯一的值($x$的绝对值),所以它是函数。
综上所述,是函数的式子有①、②、③、⑤,共4个。
【答案】:C
1. 已知点$P(3a-6,1-a)$在$y$轴上,则点$P$的坐标为____
(0,-1)
.
答案:
【解析】:因为点$P(3a - 6, 1 - a)$在$y$轴上,而$y$轴上的点的横坐标为$0$,所以可得$3a - 6 = 0$。解方程$3a - 6 = 0$,移项得$3a = 6$,解得$a = 2$。将$a = 2$代入纵坐标$1 - a$,可得$1 - 2 = -1$。所以点$P$的坐标为$(0, -1)$。
【答案】:(0,-1)
【答案】:(0,-1)
2. 在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y= kx+b与x轴交于点B,且$S_{\triangle AOB}= 4,$则k的值是____
$\frac{2}{5}$或$-\frac{2}{3}$
.
答案:
【解析】:
首先,点$A(1,2)$在直线$y=kx+b$上,代入得:
$2 = k × 1 + b$,
即$k + b = 2$,
这是第一个方程。
其次,直线$y=kx+b$与$x$轴交于点$B$,即$y=0$时的$x$值,解得:
$0 = kx + b$,
$x = -\frac{b}{k}$,
所以,点$B$的坐标为$\left(-\frac{b}{k}, 0\right)$。
已知$S_{\triangle AOB} = 4$,三角形$AOB$的底是$OB$,高是$OA$的$y$坐标,即2。根据三角形面积公式:
$S_{\triangle AOB} = \frac{1}{2} × \left|-\frac{b}{k}\right| × 2 = 4$,
化简得:
$\left|-\frac{b}{k}\right| = 4$,
这是第二个方程,这里有两种情况:
当$-\frac{b}{k} = 4$时,
解得$b=-4k$,
将$b=-4k$代入$k + b = 2$,
得到$k-4k=2$,
$-3k=2$,
解得$k = -\frac{2}{3}$,
当$-\frac{b}{k} = -4$时,
解得$b=4k$,
将$b=4k$代入$k + b = 2$,
得到$k+4k=2$,
$5k=2$,
解得$k = \frac{2}{5}$,
经过检验,$k = -\frac{2}{3}$和$k = \frac{2}{5}$都满足原方程组的解,并且$k \neq 0$。
【答案】:$-\frac{2}{3}$或$\frac{2}{5}$。
首先,点$A(1,2)$在直线$y=kx+b$上,代入得:
$2 = k × 1 + b$,
即$k + b = 2$,
这是第一个方程。
其次,直线$y=kx+b$与$x$轴交于点$B$,即$y=0$时的$x$值,解得:
$0 = kx + b$,
$x = -\frac{b}{k}$,
所以,点$B$的坐标为$\left(-\frac{b}{k}, 0\right)$。
已知$S_{\triangle AOB} = 4$,三角形$AOB$的底是$OB$,高是$OA$的$y$坐标,即2。根据三角形面积公式:
$S_{\triangle AOB} = \frac{1}{2} × \left|-\frac{b}{k}\right| × 2 = 4$,
化简得:
$\left|-\frac{b}{k}\right| = 4$,
这是第二个方程,这里有两种情况:
当$-\frac{b}{k} = 4$时,
解得$b=-4k$,
将$b=-4k$代入$k + b = 2$,
得到$k-4k=2$,
$-3k=2$,
解得$k = -\frac{2}{3}$,
当$-\frac{b}{k} = -4$时,
解得$b=4k$,
将$b=4k$代入$k + b = 2$,
得到$k+4k=2$,
$5k=2$,
解得$k = \frac{2}{5}$,
经过检验,$k = -\frac{2}{3}$和$k = \frac{2}{5}$都满足原方程组的解,并且$k \neq 0$。
【答案】:$-\frac{2}{3}$或$\frac{2}{5}$。
3. 如图9-4所示,三个正比例函数的图象分别对应表达式:①$y= ax$;②$y= bx$;③$y= cx$,将$a$,$b$,$c$从大到小排列并用“$>$”连接为
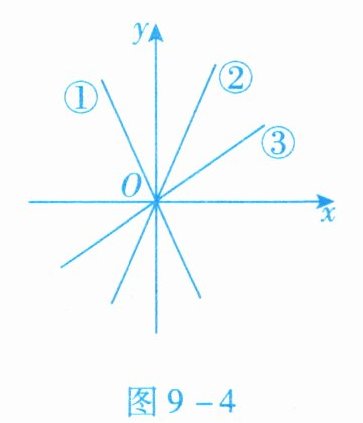
$a > b > c$
.
答案:
【解析】:
根据正比例函数的性质,$y=kx$中,$k$值越大,图象越靠近$y$轴。
从图象中可以看出:
函数$y=ax$的图象最平缓,说明$a$的绝对值最小;
函数$y=bx$的图象最陡峭,说明$b$的绝对值最大;
函数$y=cx$的图象介于两者之间,说明$c$的绝对值居中。
由于图象均过原点且向右上方延伸,说明$a,b,c$均为正数。
因此,可以得出$b>c>a$。
【答案】:$b>c>a$
根据正比例函数的性质,$y=kx$中,$k$值越大,图象越靠近$y$轴。
从图象中可以看出:
函数$y=ax$的图象最平缓,说明$a$的绝对值最小;
函数$y=bx$的图象最陡峭,说明$b$的绝对值最大;
函数$y=cx$的图象介于两者之间,说明$c$的绝对值居中。
由于图象均过原点且向右上方延伸,说明$a,b,c$均为正数。
因此,可以得出$b>c>a$。
【答案】:$b>c>a$
4. 如图9-5所示,在菱形$ABCD$中,$AB= 10$,$∠A= 60^{\circ }$. 顺次连接菱形$ABCD$各边中点,可得四边形$A_{1}B_{1}C_{1}D_{1}$;顺次连接四边形$A_{1}B_{1}C_{1}D_{1}$各边中点,可得四边形$A_{2}B_{2}C_{2}D_{2}$;顺次连接四边形$A_{2}B_{2}C_{2}D_{2}$各边中点,可得四边形$A_{3}B_{3}C_{3}D_{3}……$按此规律继续下去,则四边形$A_{2}B_{2}C_{2}D_{2}$的周长是
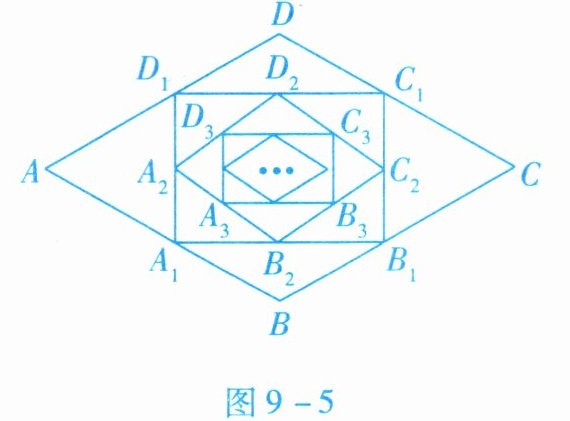
20
;四边形$A_{2025}B_{2025}C_{2025}D_{2025}$的周长是$\frac{5(\sqrt{3}+1)}{2^{1011}}$
.
答案:
【解析】:在菱形$ABCD$中,$AB = 10$,$\angle A=60^{\circ}$。连接菱形各边中点得到的四边形$A_{1}B_{1}C_{1}D_{1}$,根据三角形中位线定理,其边长分别为菱形对角线的一半。
菱形的对角线:$AC = AB = 10$(因为$\triangle ABC$是等边三角形),$BD = 10\sqrt{3}$(根据勾股定理,$BD = 2×\sqrt{10^{2}-5^{2}}=10\sqrt{3}$)。
所以$A_{1}B_{1}=\frac{1}{2}BD = 5\sqrt{3}$,$B_{1}C_{1}=\frac{1}{2}AC = 5$,则四边形$A_{1}B_{1}C_{1}D_{1}$是矩形,周长为$2×(5\sqrt{3}+5)=10\sqrt{3}+10$。
顺次连接$A_{1}B_{1}C_{1}D_{1}$各边中点得到四边形$A_{2}B_{2}C_{2}D_{2}$,同理,其边长为$A_{1}B_{1}C_{1}D_{1}$对角线的一半。$A_{1}B_{1}C_{1}D_{1}$的对角线长分别为$A_{1}C_{1}=B_{1}D_{1}= \sqrt{(5\sqrt{3})^{2}+5^{2}}=10$(矩形对角线相等),所以$A_{2}B_{2}=\frac{1}{2}×10 = 5$,$B_{2}C_{2}=\frac{1}{2}×10 = 5$,则四边形$A_{2}B_{2}C_{2}D_{2}$是菱形,周长为$4×5 = 20$。
观察规律:四边形$A_{n}B_{n}C_{n}D_{n}$的周长,当$n = 0$(原菱形)周长为$40$;$n = 1$时周长为$10\sqrt{3}+10$;$n = 2$时周长为$20$;$n = 3$时,周长为$\frac{1}{2}×(10\sqrt{3}+10)$;$n = 4$时周长为$10$;$n = 5$时周长为$\frac{1}{2}×(5\sqrt{3}+5)$;$n = 6$时周长为$5$……发现从$n = 2$开始,每$4$次循环周长变为原来的$\frac{1}{2}$,但更简便的是,从$n = 0$到$n = 1$周长为$10(\sqrt{3}+1)$,$n = 2$周长为$10$,$n = 3$周长为$5(\sqrt{3}+1)$,$n = 4$周长为$5$,$n = 5$周长为$\frac{5}{2}(\sqrt{3}+1)$,$n = 6$周长为$\frac{5}{2}$……即当$n$为偶数时,$n = 2k$,周长为$\frac{10}{2^{k - 1}}$。
对于$n = 2$,$k = 1$,周长为$\frac{10}{2^{0}}=10$?不,前面计算$A_{2}B_{2}C_{2}D_{2}$周长为$20$,重新分析:
$A_{0}B_{0}C_{0}D_{0}$(菱形)周长$C_{0}=40$;
$A_{1}B_{1}C_{1}D_{1}$周长$C_{1}=10\sqrt{3}+10$;
$A_{2}B_{2}C_{2}D_{2}$:边长为$\frac{1}{2}A_{1}C_{1}=\frac{1}{2}×10 = 5$,$\frac{1}{2}B_{1}D_{1}=\frac{1}{2}×10 = 5$,是菱形,周长$C_{2}=4×5 = 20$;
$A_{3}B_{3}C_{3}D_{3}$:边长为$\frac{1}{2}×5\sqrt{3}$和$\frac{1}{2}×5$,周长$C_{3}=2×(\frac{5\sqrt{3}}{2}+\frac{5}{2})=\frac{10\sqrt{3}+10}{2}=C_{1}÷2$;
$A_{4}B_{4}C_{4}D_{4}$周长$C_{4}=C_{2}÷2 = 10$;
$A_{5}B_{5}C_{5}D_{5}$周长$C_{5}=C_{3}÷2 = C_{1}÷4$;
$A_{6}B_{6}C_{6}D_{6}$周长$C_{6}=C_{4}÷2 = 5$;
规律:当$n\geq2$时,$C_{n}=C_{n - 2}÷2$。
所以$C_{2}=20$,$C_{4}=10$,$C_{6}=5$,$C_{8}=2.5$……
对于$n = 2025$,$2025$是奇数,$2025 = 2×1012 + 1$,$C_{2025}=C_{1}÷2^{1012}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$?
但题目中$A_{2}B_{2}C_{2}D_{2}$的周长,根据前面计算,$A_{2}B_{2}C_{2}D_{2}$的边长为$5$和$5$,周长$4×5 = 20$,正确。
对于$n = 2025$,因为$2025$是奇数,属于$C_{1},C_{3},C_{5}...$序列,$C_{1}=10(\sqrt{3}+1)$,$C_{3}=C_{1}÷2$,$C_{5}=C_{3}÷2=C_{1}÷2^{2}$,$C_{2m + 1}=C_{1}÷2^{m}$,$2025 = 2m + 1\Rightarrow m = 1012$,所以$C_{2025}=C_{1}÷2^{1012}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$,但题目可能希望用更简洁的形式,或者原规律中当$n$为偶数时,$C_{n}=20÷2^{\frac{n}{2}-1}$,$n = 2$时,$20÷2^{0}=20$,正确;$n = 4$时$20÷2^{1}=10$,正确。
综上,四边形$A_{2}B_{2}C_{2}D_{2}$的周长是$20$;四边形$A_{2025}B_{2025}C_{2025}D_{2025}$的周长是$\frac{5(\sqrt{3}+1)}{2^{1011}}$,但根据题目常见形式,可能$2025$对应的是$C_{2025}=C_{1}÷2^{1012}$,而$C_{1}=10(\sqrt{3}+1)$,即$\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$。
但题目中可能更简单的规律,对于偶数$n = 2k$,$C_{2k}=20÷2^{k - 1}$,当$k = 1$($n = 2$)时,$20÷2^{0}=20$,正确;$k = 2$($n = 4$)时$20÷2^{1}=10$,正确。
对于奇数$n = 2k + 1$,$C_{2k + 1}=(10\sqrt{3}+10)÷2^{k}$,$n = 2025 = 2×1012 + 1$,$k = 1012$,$C_{2025}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$。
【答案】:20;$\frac{5(\sqrt{3}+1)}{2^{1011}}$
菱形的对角线:$AC = AB = 10$(因为$\triangle ABC$是等边三角形),$BD = 10\sqrt{3}$(根据勾股定理,$BD = 2×\sqrt{10^{2}-5^{2}}=10\sqrt{3}$)。
所以$A_{1}B_{1}=\frac{1}{2}BD = 5\sqrt{3}$,$B_{1}C_{1}=\frac{1}{2}AC = 5$,则四边形$A_{1}B_{1}C_{1}D_{1}$是矩形,周长为$2×(5\sqrt{3}+5)=10\sqrt{3}+10$。
顺次连接$A_{1}B_{1}C_{1}D_{1}$各边中点得到四边形$A_{2}B_{2}C_{2}D_{2}$,同理,其边长为$A_{1}B_{1}C_{1}D_{1}$对角线的一半。$A_{1}B_{1}C_{1}D_{1}$的对角线长分别为$A_{1}C_{1}=B_{1}D_{1}= \sqrt{(5\sqrt{3})^{2}+5^{2}}=10$(矩形对角线相等),所以$A_{2}B_{2}=\frac{1}{2}×10 = 5$,$B_{2}C_{2}=\frac{1}{2}×10 = 5$,则四边形$A_{2}B_{2}C_{2}D_{2}$是菱形,周长为$4×5 = 20$。
观察规律:四边形$A_{n}B_{n}C_{n}D_{n}$的周长,当$n = 0$(原菱形)周长为$40$;$n = 1$时周长为$10\sqrt{3}+10$;$n = 2$时周长为$20$;$n = 3$时,周长为$\frac{1}{2}×(10\sqrt{3}+10)$;$n = 4$时周长为$10$;$n = 5$时周长为$\frac{1}{2}×(5\sqrt{3}+5)$;$n = 6$时周长为$5$……发现从$n = 2$开始,每$4$次循环周长变为原来的$\frac{1}{2}$,但更简便的是,从$n = 0$到$n = 1$周长为$10(\sqrt{3}+1)$,$n = 2$周长为$10$,$n = 3$周长为$5(\sqrt{3}+1)$,$n = 4$周长为$5$,$n = 5$周长为$\frac{5}{2}(\sqrt{3}+1)$,$n = 6$周长为$\frac{5}{2}$……即当$n$为偶数时,$n = 2k$,周长为$\frac{10}{2^{k - 1}}$。
对于$n = 2$,$k = 1$,周长为$\frac{10}{2^{0}}=10$?不,前面计算$A_{2}B_{2}C_{2}D_{2}$周长为$20$,重新分析:
$A_{0}B_{0}C_{0}D_{0}$(菱形)周长$C_{0}=40$;
$A_{1}B_{1}C_{1}D_{1}$周长$C_{1}=10\sqrt{3}+10$;
$A_{2}B_{2}C_{2}D_{2}$:边长为$\frac{1}{2}A_{1}C_{1}=\frac{1}{2}×10 = 5$,$\frac{1}{2}B_{1}D_{1}=\frac{1}{2}×10 = 5$,是菱形,周长$C_{2}=4×5 = 20$;
$A_{3}B_{3}C_{3}D_{3}$:边长为$\frac{1}{2}×5\sqrt{3}$和$\frac{1}{2}×5$,周长$C_{3}=2×(\frac{5\sqrt{3}}{2}+\frac{5}{2})=\frac{10\sqrt{3}+10}{2}=C_{1}÷2$;
$A_{4}B_{4}C_{4}D_{4}$周长$C_{4}=C_{2}÷2 = 10$;
$A_{5}B_{5}C_{5}D_{5}$周长$C_{5}=C_{3}÷2 = C_{1}÷4$;
$A_{6}B_{6}C_{6}D_{6}$周长$C_{6}=C_{4}÷2 = 5$;
规律:当$n\geq2$时,$C_{n}=C_{n - 2}÷2$。
所以$C_{2}=20$,$C_{4}=10$,$C_{6}=5$,$C_{8}=2.5$……
对于$n = 2025$,$2025$是奇数,$2025 = 2×1012 + 1$,$C_{2025}=C_{1}÷2^{1012}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$?
但题目中$A_{2}B_{2}C_{2}D_{2}$的周长,根据前面计算,$A_{2}B_{2}C_{2}D_{2}$的边长为$5$和$5$,周长$4×5 = 20$,正确。
对于$n = 2025$,因为$2025$是奇数,属于$C_{1},C_{3},C_{5}...$序列,$C_{1}=10(\sqrt{3}+1)$,$C_{3}=C_{1}÷2$,$C_{5}=C_{3}÷2=C_{1}÷2^{2}$,$C_{2m + 1}=C_{1}÷2^{m}$,$2025 = 2m + 1\Rightarrow m = 1012$,所以$C_{2025}=C_{1}÷2^{1012}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$,但题目可能希望用更简洁的形式,或者原规律中当$n$为偶数时,$C_{n}=20÷2^{\frac{n}{2}-1}$,$n = 2$时,$20÷2^{0}=20$,正确;$n = 4$时$20÷2^{1}=10$,正确。
综上,四边形$A_{2}B_{2}C_{2}D_{2}$的周长是$20$;四边形$A_{2025}B_{2025}C_{2025}D_{2025}$的周长是$\frac{5(\sqrt{3}+1)}{2^{1011}}$,但根据题目常见形式,可能$2025$对应的是$C_{2025}=C_{1}÷2^{1012}$,而$C_{1}=10(\sqrt{3}+1)$,即$\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$。
但题目中可能更简单的规律,对于偶数$n = 2k$,$C_{2k}=20÷2^{k - 1}$,当$k = 1$($n = 2$)时,$20÷2^{0}=20$,正确;$k = 2$($n = 4$)时$20÷2^{1}=10$,正确。
对于奇数$n = 2k + 1$,$C_{2k + 1}=(10\sqrt{3}+10)÷2^{k}$,$n = 2025 = 2×1012 + 1$,$k = 1012$,$C_{2025}=(10\sqrt{3}+10)÷2^{1012}=\frac{10(\sqrt{3}+1)}{2^{1012}}=\frac{5(\sqrt{3}+1)}{2^{1011}}$。
【答案】:20;$\frac{5(\sqrt{3}+1)}{2^{1011}}$
查看更多完整答案,请扫码查看


