第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
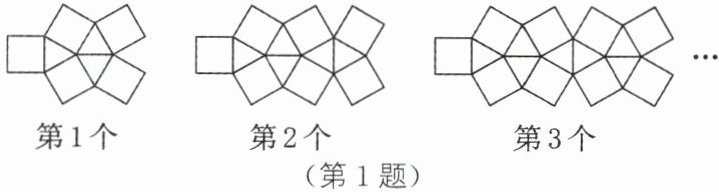
1. 用边长相等的正方形和等边三角形按如图所示的规律摆放,其中第1个图案中有5个正方形,第2个图案中有7个正方形,第3个图案中有9个正方形……按此规律排列下去,则第2025个图案中正方形的个数是 (
...
A.4048
B.4049
C.4051
D.4053
D
)...

A.4048
B.4049
C.4051
D.4053
答案:
D 解析:由题图,可知第1个图案中正方形的个数为$5=1×2+3$;第2个图案中正方形的个数为$7=2×2+3$;第3个图案中正方形的个数为$9=3×2+3$…,所以第n个图案中正方形的个数为$2n+3$.当$n=2025$时,$2n+3=2×2025+3=4053$,即第2025个图案中正方形的个数为4053.
2. 数轴上的点A,B,C,D分别表示数a,b,c,d,已知点A在点B的左侧,点C在点B的左侧,点D在点B,C之间,则下列式子中,可能成立的是 (
A.$a<b<c<d$
B.$b<c<d<a$
C.$c<d<a<b$
D.$c<d<b<a$
C
)A.$a<b<c<d$
B.$b<c<d<a$
C.$c<d<a<b$
D.$c<d<b<a$
答案:
C 解析:因为点A在点B的左侧,所以a<b.因为点C在点B的左侧,所以c<b.因为点D在点B,C之间,所以c<d<b.所以可能成立的是c<d<a<b.
3. (2024·北京)为助力数字经济发展,北京积极推进多个公共算力中心的建设.北京数字经济算力中心目前已部署上架和调试的设备的算力为$4×10^{17}$Flops(Flops是计算机系统算力的一种度量单位),整体投产后,累计实现的算力将是目前已部署上架和调试的设备的算力的5倍,达到m Flops,则m的值为 (
A.$8×10^{16}$
B.$2×10^{17}$
C.$5×10^{17}$
D.$2×10^{18}$
D
)A.$8×10^{16}$
B.$2×10^{17}$
C.$5×10^{17}$
D.$2×10^{18}$
答案:
D
4. 一个盖着瓶盖的瓶子里面装着一些水(如图),根据图中的数据,可得瓶子的容积是
70
$cm^{3}$.
答案:
70 解析:由题意,易得瓶子的容积$=10×5+10×(9-7)=70(cm^3)$.
5. (2023·宜兴段考)点A在数轴上表示4,与点A距离为3的点B表示的数为
7或1
;在数轴上,到原点距离不大于2的所有整数有-2,-1,0,1,2
.
答案:
7或1 -2,-1,0,1,2
6. 若$(a-4)^{2}+|a+b-3|= 0$,则$b^{a}=$
1
.
答案:
1 解析:因为$(a-4)^2+|a+b-3|=0$,$(a-4)^2\geq0$,$|a+b-3|\geq0$,所以$a-4=0$,$a+b-3=0$.所以a=4,b=-1.所以$b^a=(-1)^4=1$.
7. 已知a,b为有理数,$|a|= 3$,$|b|= 5$,且$|a+b|= -a-b$,则$a-b$的值为
8或2
.
答案:
8或2 解析:因为a,b为有理数,|a|=3,|b|=5,所以$a=\pm3$,$b=\pm5$.因为$|a+b|=-a-b$,所以$a+b\leq0$.所以$a=\pm3$,$b=-5$.当a=3,b=-5时,$a-b=8$;当a=-3,b=-5时,$a-b=2$.所以a-b的值为8或2.
8. 用$(x,y)$表示x,y两数中较大的一个数,用$[x,y]$表示x,y两数中较小的一个数,则$(-5,-0.5)-[-3,2]$的值为
2.5
.
答案:
2.5 解析:因为(x,y)表示x,y两数中较大的一个数,-5<-0.5,所以(-5,-0.5)=-0.5.因为[x,y]表示x,y两数中较小的一个数,-3<2,所以[-3,2]=-3.所以$(-5,-0.5)-[-3,2]=-0.5-(-3)=-0.5+3=2.5$.
9. 出租车司机刘师傅某天上午从A地出发,在东西方向笔直的公路上行驶营运,表中记录的是上午每次行驶的里程(单位:千米,规定向东走为正,向西走为负;×表示空载,○表示载有乘客,且乘客都不相同):
|次序|1|2|3|4|5|6|7|8|
|里程|-3|-15|+19|-1|+5|-12|-6|+12|
|载客|×|○|○|×|○|○|○|○|
(1) 刘师傅走完第8次营运后,他在A地的什么方向,离A地有多少千米?
(2) 已知出租车每千米耗油约0.06升,刘师傅开始营运前油箱里有8升油,若少于2升则需要加油,请通过计算说明刘师傅这天上午中途是否可以不加油.
(3) 已知载客时3千米及以内收费15元,超过3千米后,超出部分每千米收费2.8元,问:刘师傅这天上午最高一次的营业额是多少元?
|次序|1|2|3|4|5|6|7|8|
|里程|-3|-15|+19|-1|+5|-12|-6|+12|
|载客|×|○|○|×|○|○|○|○|
(1) 刘师傅走完第8次营运后,他在A地的什么方向,离A地有多少千米?
(2) 已知出租车每千米耗油约0.06升,刘师傅开始营运前油箱里有8升油,若少于2升则需要加油,请通过计算说明刘师傅这天上午中途是否可以不加油.
(3) 已知载客时3千米及以内收费15元,超过3千米后,超出部分每千米收费2.8元,问:刘师傅这天上午最高一次的营业额是多少元?
答案:
(1)$-3-15+19-1+5-12-6+12=-1$(千米), 所以刘师傅走完第8次营运后,他在A地的西边,离A地有1千米.
(2)刘师傅这天上午行驶的总里程为$|-3|+|-15|+|+19|+|-1|+|+5|+|-12|+|-6|+|+12|=73$(千米),耗油量为$0.06×73=4.38$(升),$8-4.38=3.62$(升),$3.62>2$, 所以刘师傅这天上午中途可以不加油.
(3)由表,知刘师傅这天上午第3次的营业额最高,第3次的营业额为$15+(19-3)×2.8=59.8$(元), 所以刘师傅这天上午最高一次的营业额是59.8元.
(1)$-3-15+19-1+5-12-6+12=-1$(千米), 所以刘师傅走完第8次营运后,他在A地的西边,离A地有1千米.
(2)刘师傅这天上午行驶的总里程为$|-3|+|-15|+|+19|+|-1|+|+5|+|-12|+|-6|+|+12|=73$(千米),耗油量为$0.06×73=4.38$(升),$8-4.38=3.62$(升),$3.62>2$, 所以刘师傅这天上午中途可以不加油.
(3)由表,知刘师傅这天上午第3次的营业额最高,第3次的营业额为$15+(19-3)×2.8=59.8$(元), 所以刘师傅这天上午最高一次的营业额是59.8元.
查看更多完整答案,请扫码查看


