《2025年拔尖特训七年级数学上册苏科版》

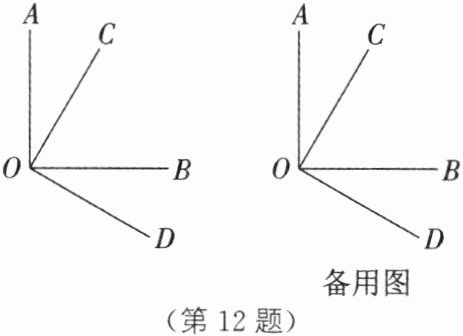
12. 如图,射线 OC 在∠AOB 的内部,射线 OD 在∠AOB 的外部,且∠AOB 与∠COD 互补,∠AOC= ∠BOD.
(1)若∠BOD= 30°,求∠BOC 的度数.
(2)若 OB 平分∠COD,求∠BOC 的度数.
(3)若射线 OE 满足∠COE：∠AOE= 1：2,请写出∠COE 与∠AOD 之间的数量关系,并说明理由.

答案：
因为∠AOB与∠COD互补，所以∠AOB+∠COD=180°，即∠AOC+∠BOC+∠BOC+∠BOD=180°.因为∠AOC=∠BOD，所以2∠AOC+2∠BOC=180°.所以∠AOC+∠BOC=90°，即∠AOB=90°.所以∠COD=90°.
(1)因为∠BOD=30°，所以∠BOC=∠COD−∠BOD=60°.
(2)因为OB平分∠COD，∠COD=90°，所以∠BOC= $\frac{1}{2}$∠COD=45°.
(3)∠AOD−∠COE=90°或∠AOD−3∠COE=90°.
理由:如图①，OE在∠AOC的外部.因为∠COE：∠AOE=1：2，所以∠COE=∠AOC.因为∠AOD=∠COD+∠AOC，所以∠AOD=90°+∠COE，即∠AOD−∠COE=90°.
如图②，OE在∠AOC的内部.因为∠COE：∠AOE=1：2，所以∠AOC=3∠COE.因为∠AOD=∠COD+∠AOC，所以∠AOD=90°+3∠COE，即∠AOD−3∠COE=90°.
综上所述，∠AOD−∠COE=90°或∠AOD−3∠COE=90°.
　

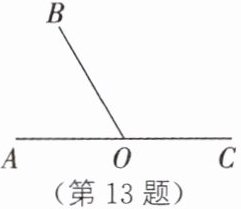
13. *如图,在平面内,O 是直线 AC 上一点,∠AOB= 60°,射线 OC 不动,射线 OA,OB 同时开始绕点 O 按顺时针方向转动,射线 OA 首次回到起始位置时两射线同时停止转动,射线 OA,OB 的转动速度分别为每秒 40°和每秒 20°. 若转动 t 秒时,射线 OA,OB,OC 中的一条是由另外两条组成的角的平分线,则 t= ______4或5.

答案： 4或5　解析:①当OA是OB，OC组成的角的平分线时，∠AOC=∠AOB.由题意，得∠AOC=(180 - 40t)°，∠AOB=(20t−60)°，则20t - 60=180−40t，解得t=4.②当OC是OB，OA组成的角的平分线时，∠AOC=∠BOC.由题意，得∠AOC=(40t−180)°，∠BOC=(120−20t)°，则40t−180=120−20t，解得t=5.③当OB是OC，OA组成的角的平分线时，∠BOC=∠AOB= $\frac{1}{2}$∠AOC.由题意，得∠BOC=(20t−120)°，∠AOB= $\frac{1}{2}$∠AOC= $\frac{1}{2}$（40t°−180°）=(20t−90)°，则20t−120=20t−90，方程无解.综上所述，t的值为4或5.
方法归纳
解决动态型问题的一般方法
解决动态型问题的一般方法是根据问题的条件画出示意图，将动态问题转化为静止问题，并根据其中的数量关系建立等量关系式求得结果.由于OA，OB都是转动的，可分为三种情况讨论：①当OA是OB，OC组成的角的平分线时；②当OC是OB，OA组成的角的平分线时；③当OB是OC，OA组成的角的平分线时.

14. (2023·扬州江都段考)如图①,O 是直线 AB 上的一点,∠COD 是直角,OE 平分∠BOC.
(1)若∠AOC= 30°,则∠BOD= 60°,∠DOE= 15°.
(2)将图①中的∠COD 绕顶点 O 按顺时针方向旋转至如图②所示的位置,其他条件不变,若∠AOC= α,求∠DOE 的度数(用含 α 的式子表示).
因为∠AOC=α，所以∠BOC=180°−α.因为OE平分∠BOC，所以∠COE= $\frac{1}{2}$∠BOC=90°− $\frac{1}{2}$α.所以∠DOE=∠COD−∠COE=90°−(90°− $\frac{1}{2}$α)= $\frac{1}{2}$α.
(3)将图①中的∠COD 绕顶点 O 按顺时针方向旋转至如图③所示的位置,其他条件不变,直接写出∠AOC 和∠DOE 之间的数量关系：∠AOC=360°−2∠DOE.

答案：
(1)60;15.　解析:因为O是直线AB上的一点，∠COD是直角，∠AOC=30°，所以∠BOD=180°−∠AOC−∠COD=60°.因为∠COD=90°，∠BOD=60°，所以∠BOC=∠COD+∠BOD=150°.因为OE平分∠BOC，所以∠BOE= $\frac{1}{2}$∠BOC=75°.所以∠DOE=∠BOE−∠BOD=75°−60°=15°.
(2)因为∠AOC=α，所以∠BOC=180°−α.因为OE平分∠BOC，所以∠COE= $\frac{1}{2}$∠BOC=90°− $\frac{1}{2}$α.所以∠DOE=∠COD−∠COE=90°−(90°− $\frac{1}{2}$α)= $\frac{1}{2}$α.
(3)∠AOC=360°−2∠DOE.
解析:设∠AOC=x，则∠BOC=180°−x.因为OE平分∠BOC，所以∠COE= $\frac{1}{2}$∠BOC=90°− $\frac{1}{2}$x.所以∠DOE=∠COD+∠COE=90°+90°− $\frac{1}{2}$x=180°− $\frac{1}{2}$x.所以∠DOE=180°− $\frac{1}{2}$∠AOC.所以∠AOC=360°−2∠DOE.