第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
1. 如图,把三角形剪去一个角,所得四边形的周长比原三角形的周长小,能正确解释这一现象的数学知识是(
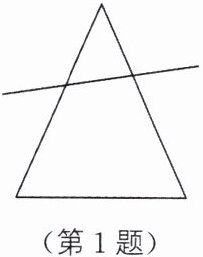
A.线动成面
B.两点之间,线段最短
C.经过一点有无数条直线
D.两点确定一条直线
]
B
)
A.线动成面
B.两点之间,线段最短
C.经过一点有无数条直线
D.两点确定一条直线
]
答案:
B
2. 如图,下列说法中,不正确的是(
A.直线MN与直线NM是同一条直线
B.射线PM与射线MP是同一条射线
C.射线PM与射线PN是同一条射线
D.线段MN与线段NM是同一条线段
B
)A.直线MN与直线NM是同一条直线
B.射线PM与射线MP是同一条射线
C.射线PM与射线PN是同一条射线
D.线段MN与线段NM是同一条线段
答案:
B
3. 如图,图中共有
2
条直线,13
条射线,6
条线段.
答案:
2 13 6
4. 值日生小明想把教室内的桌椅摆放整齐,为了将一列课桌摆放整齐,他把这列课桌的最前面一张和最后面一张先排在一条线上,其余课桌按这条线摆放,这样做用到的数学知识为
两点确定一条直线
.
答案:
两点确定一条直线
5. 如图,平面上有四个点A,B,C,D,根据下列语句画图.
(1)画直线AB.
(2)画射线AD.
(3)画直线CD,交直线AB于点E.
(4)连接AC,BD,相交于点F.
]
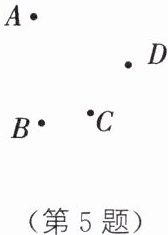
(1)画直线AB.
(2)画射线AD.
(3)画直线CD,交直线AB于点E.
(4)连接AC,BD,相交于点F.
]
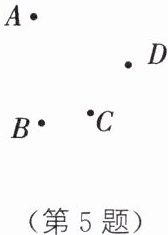
答案:
(1)~
(4)如图所示,

(1)~
(4)如图所示,

6. A,B,C,D,E五个景点之间的路线如图所示.若每条路线的里程a(km)及行驶的平均速度b(km/h)用(a,b)表示,则从景点A到景点C用时最少的路线是(
A.A→E→C
B.A→B→C
C.A→E→B→C
D.A→B→E→C
D
)A.A→E→C
B.A→B→C
C.A→E→B→C
D.A→B→E→C
答案:
D 解析:A→E→C:80÷40+200÷100=4(h);A→B→C:100÷100+180÷60=4(h);A→E→B→C:80÷40+50÷100+180÷60=5.5(h);A→B→E→C:100÷100+50÷100+200÷100=3.5(h). 因为3.5<4<5.5,所以从景点A到景点C用时最少的路线是A→B→E→C.
7. 已知线段AB= 6,点C在直线AB上,AB= 3BC,则点A,C之间的距离为______.
答案:
8或4 解析:因为AB=3BC,AB=6,所以BC=$\frac{1}{3}$AB=$\frac{1}{3}$×6=2. 如图①,当点C在射线AB上时,AC=AB+BC=6+2=8. 如图②,当点C在线段AB上时,AC=AB-BC=6-2=4. 当点C在射线BA上时,显然不成立. 综上所述,点A,C之间的距离为8或4.

8或4 解析:因为AB=3BC,AB=6,所以BC=$\frac{1}{3}$AB=$\frac{1}{3}$×6=2. 如图①,当点C在射线AB上时,AC=AB+BC=6+2=8. 如图②,当点C在线段AB上时,AC=AB-BC=6-2=4. 当点C在射线BA上时,显然不成立. 综上所述,点A,C之间的距离为8或4.

8. 火车票价与两站之间的铁路里程有关,里程越长,票价越高.如果一段铁路上共有5个站点,每两站间的里程都不相等,那么这段铁路上的火车票价共有
10
种.
答案:
10 解析:这段铁路上的火车票价共有4+3+2+1=10(种).
9. 直线上有2020个点,我们进行如下操作:在每相邻两个点间插入1个点,经过3次这样的操作后,直线上共有
16153
个点.
答案:
16153 解析:第1次:2020+(2020-1)=2×2020-1;第2次:(2×2020-1)+(2×2020-1-1)=4×2020-3;第3次:(4×2020-3)+(4×2020-3-1)=8×2020-7,所以经过3次这样的操作后,直线上共有8×2020-7=16153(个)点.
10. 已知平面上有点A,B,C,D(每三点都不在一条直线上).
(1)经过这四点最多能确定
(2)如图,A,B,C,D四点表示公园里的四个地方,如果点B,C在公园里湖对岸两处,点A,D在湖面上,要从点B到点C筑桥,有①②两条路线.从节省材料的角度考虑,应选择哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
]
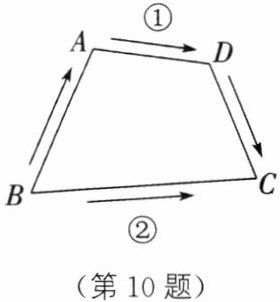
(1)经过这四点最多能确定
6
条直线.(2)如图,A,B,C,D四点表示公园里的四个地方,如果点B,C在公园里湖对岸两处,点A,D在湖面上,要从点B到点C筑桥,有①②两条路线.从节省材料的角度考虑,应选择哪一条?如果有人想在桥上较长时间观赏湖面风光,应选择哪一条?为什么?
]

(2) 从节省材料的角度考虑,应选择路线②;如果有人想在桥上较长时间观赏湖面风光,应选择路线①. 因为两点之间,线段最短,路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光.
答案:
(1) 6.
(2) 从节省材料的角度考虑,应选择路线②;如果有人想在桥上较长时间观赏湖面风光,应选择路线①. 因为两点之间,线段最短,路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光.
(1) 6.
(2) 从节省材料的角度考虑,应选择路线②;如果有人想在桥上较长时间观赏湖面风光,应选择路线①. 因为两点之间,线段最短,路线②比路线①短,可以节省材料;而路线①较长,可以在桥上较长时间观赏湖面风光.
查看更多完整答案,请扫码查看


