《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

16. (8分)已知某二次函数的图象的顶点坐标为$(-2, 2)$，且过点$(-1, 3)$.
(1)求此二次函数的解析式；
(2)判断点$P(1, 9)$是否在这个二次函数的图象上，并说明理由.

答案： 16.解：
(1)
∵二次函数的图象的顶点坐标为$(-2,2)$，
∴设二次函数的解析式为$y = a(x + 2)^{2}+2$。
将点$(-1,3)$代入，得$(-1 + 2)^{2}a + 2 = 3$。解得$a = 1$。
∴二次函数的解析式为$y=(x + 2)^{2}+2=x^{2}+4x + 6$。
(2)点$P(1,9)$不在这个二次函数的图象上。
理由：把$x = 1$代入$y = x^{2}+4x + 6$，得$y = 1 + 4 + 6 = 11$。
∵$9\neq11$，
∴点$P(1,9)$不在这个二次函数的图象上。

17. 〔南阳市〕(9分)抛物线$y = ax^2 - 2ax + 1(a ＞ 0)$经过点$A(x_1, y_1)$，$B(x_2, y_2)$，其中$x_1 ＜ x_2$.
(1)求该抛物线的对称轴；
(2)若$y_1 = y_2 = 1$，直接写出$x_1$，$x_2$的值；
(3)若$-1 ＜ x_1 ＜ 0$，$1 ＜ x_2 ＜ 2$，试比较$y_1$与$y_2$的大小，并说明理由.

答案： 17.解：
(1)
∵$y = ax^{2}-2ax + 1 = a(x - 1)^{2}-a + 1$，
∴抛物线的对称轴为直线$x = 1$。
(2)$x_{1}=0$，$x_{2}=2$。
(3)方法一：$y_{1}＞y_{2}$。
理由：由
(1)可知，抛物线的对称轴为直线$x = 1$，且$a＞0$。
∴当$x＜1$时，$y$随$x$的增大而减小，当$x＞1$时，$y$随$x$的增大而增大。
∵$-1＜x_{1}＜0$，$1＜x_{2}＜2$，
∴$1＜1 - x_{1}＜2$，$0＜x_{2}-1＜1$。
结合函数图象可知，当抛物线开口向上时，距离对称轴越远，函数值越大，
∴$y_{1}＞y_{2}$。
方法二：$y_{1}＞y_{2}$。
理由：
∵$-1＜x_{1}＜0$，$1＜x_{2}＜2$，
∴$x_{1}-x_{2}＜0$，$0＜x_{1}+x_{2}＜2$。
∴$x_{1}+x_{2}-2＜0$。
∴$y_{1}-y_{2}=(ax_{1}^{2}-2ax_{1}+1)-(ax_{2}^{2}-2ax_{2}+1)=a(x_{1}-x_{2})(x_{1}+x_{2}-2)＞0$。
∴$y_{1}＞y_{2}$。

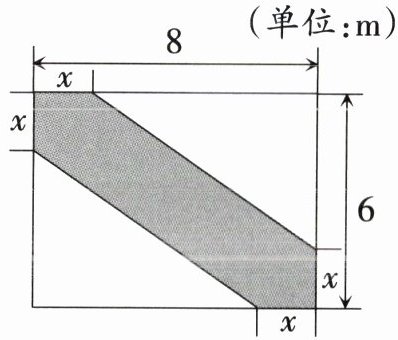
18. (9分)如图，某景区内有一块矩形鲜花田地，其长为8 m，宽为6 m.现在其中修建一条观花道(图中阴影部分，观花道在矩形田地的长与宽上的长度均为$x$ m)供游人赏花，设改建后剩余鲜花占地面积为$y$ m².
(1)求$y$与$x$的函数关系式，并写出自变量的取值范围；
(2)若改建后观花道的面积为13 m²，求$x$的值.

答案： 18.解：
(1)根据题意，得$y=\frac{1}{2}(8 - x)(6 - x)×2 = x^{2}-14x + 48(0＜x＜6)$。
∴$y$与$x$的函数关系式为$y = x^{2}-14x + 48(0＜x＜6)$。
(2)根据题意，得$6×8-(x^{2}-14x + 48)=13$。
解得$x_{1}=1$，$x_{2}=13$(舍去)。
∴$x$的值为$1$。