2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
8.[河北中考] 某款“不倒翁”(图1)从正面看如图2所示,PA,PB分别与$\overset{\frown}{AMB}$所在圆相切于点A,B. 若该圆半径是9 cm,$\angle P = 40^{\circ}$,则$\overset{\frown}{AMB}$的长是 (
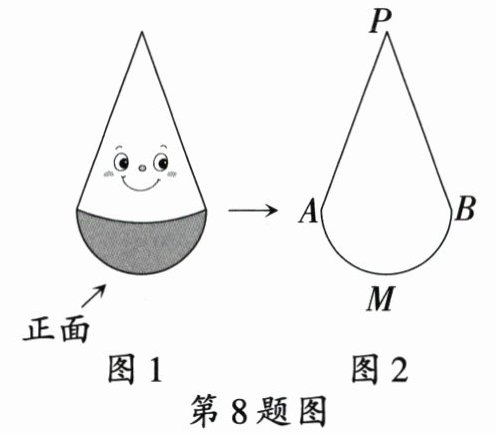
A.$11\pi$ cm
B.$\frac{11}{2} \pi$ cm
C.$7\pi$ cm
D.$\frac{7}{2} \pi$ cm
A
)
A.$11\pi$ cm
B.$\frac{11}{2} \pi$ cm
C.$7\pi$ cm
D.$\frac{7}{2} \pi$ cm
答案:
8.A [解析]如图,设点O为$\widehat{AMB}$所在圆的圆心.

根据题意,得OA⊥PA,OB⊥PB.
∴∠OAP=∠OBP=90°.
∵∠P = 40°,
∴∠AOB = 140°.
∴$\widehat{AMB}$对应的圆心角为360° - 140° = 220°.
∴$\widehat{AMB}$的长是$\frac{220\pi×9}{180}$ = 11π(cm).故选A.
8.A [解析]如图,设点O为$\widehat{AMB}$所在圆的圆心.

根据题意,得OA⊥PA,OB⊥PB.
∴∠OAP=∠OBP=90°.
∵∠P = 40°,
∴∠AOB = 140°.
∴$\widehat{AMB}$对应的圆心角为360° - 140° = 220°.
∴$\widehat{AMB}$的长是$\frac{220\pi×9}{180}$ = 11π(cm).故选A.
9. 如图,⊙P与x轴交于点A(-5,0),B(1,0),与y轴的正半轴交于点C. 若$\angle ACB = 60^{\circ}$,则点P的坐标为 (
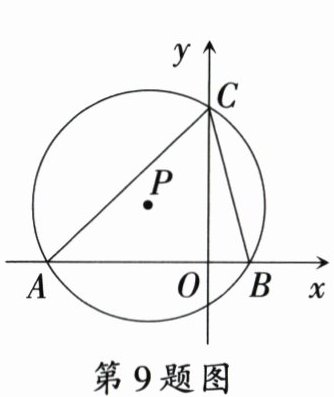
A.$(-3,\sqrt{3})$
B.$(-2,\sqrt{3})$
C.$(-3,3\sqrt{3})$
D.$(-2,3\sqrt{3})$
B
)
A.$(-3,\sqrt{3})$
B.$(-2,\sqrt{3})$
C.$(-3,3\sqrt{3})$
D.$(-2,3\sqrt{3})$
答案:
9.B
10.[安阳市改编] 如图,在$ Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 1$,$\angle A = 60^{\circ}$,将$ Rt\triangle ABC$绕点C顺时针旋转$90^{\circ}$后得到$ Rt\triangle DEC$,点B经过的路径为$\overset{\frown}{BE}$,将线段AB绕点A顺时针旋转$60^{\circ}$后,点B恰好落在CE上的点F处,点B经过的路径为$\overset{\frown}{BF}$,则图中阴影部分的面积是 (
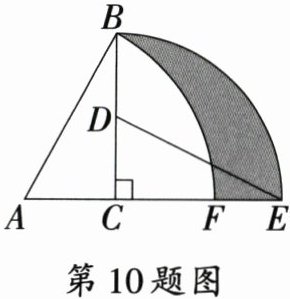
A.$\frac{\sqrt{3}}{2} + \frac{\pi}{12}$
B.$\frac{\sqrt{3}}{2} - \frac{\pi}{12}$
C.$\sqrt{3} + \frac{\pi}{12}$
D.$\sqrt{3} - \frac{\pi}{12}$
A
)
A.$\frac{\sqrt{3}}{2} + \frac{\pi}{12}$
B.$\frac{\sqrt{3}}{2} - \frac{\pi}{12}$
C.$\sqrt{3} + \frac{\pi}{12}$
D.$\sqrt{3} - \frac{\pi}{12}$
答案:
10.A [解析]
∵∠ACB = 90°,∠A = 60°,
∴∠ABC = 30°.
∵AC = 1,
∴AB = 2AC = 2.
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{3}$.根据旋转的性质,得∠BCE = 90°,AF = AB = 2,CE = BC = $\sqrt{3}$.
∴$S_{阴影}$ = $S_{\triangle ACB}$ + $S_{扇形CBE}$ - $S_{扇形ABF}$ = $\frac{1}{2}×1×\sqrt{3}$ + $\frac{90\pi×(\sqrt{3})^{2}}{360}$ - $\frac{60\pi×2^{2}}{360}$ = $\frac{\sqrt{3}}{2}$ + $\frac{3\pi}{4}$ - $\frac{2\pi}{3}$ = $\frac{\sqrt{3}}{2}$ + $\frac{\pi}{12}$.故选A.
∵∠ACB = 90°,∠A = 60°,
∴∠ABC = 30°.
∵AC = 1,
∴AB = 2AC = 2.
∴BC = $\sqrt{AB^{2}-AC^{2}}$ = $\sqrt{3}$.根据旋转的性质,得∠BCE = 90°,AF = AB = 2,CE = BC = $\sqrt{3}$.
∴$S_{阴影}$ = $S_{\triangle ACB}$ + $S_{扇形CBE}$ - $S_{扇形ABF}$ = $\frac{1}{2}×1×\sqrt{3}$ + $\frac{90\pi×(\sqrt{3})^{2}}{360}$ - $\frac{60\pi×2^{2}}{360}$ = $\frac{\sqrt{3}}{2}$ + $\frac{3\pi}{4}$ - $\frac{2\pi}{3}$ = $\frac{\sqrt{3}}{2}$ + $\frac{\pi}{12}$.故选A.
11.[洛阳市] 如图,一个直角三角板的$30^{\circ}$角的顶点P落在⊙O上,两边分别交⊙O于点A,B,且BP过圆心O,连接AB. 若⊙O的直径为4,则弦AB的长为
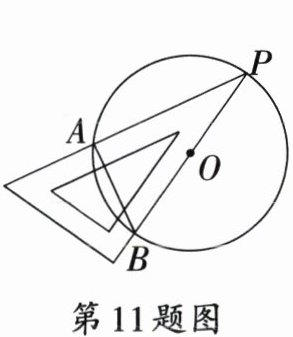
2
.
答案:
11.2
12. 某同学在数学实践活动中,制作了一个侧面积为$21\pi cm^2$的圆锥. 已知圆锥的母线长为7 cm,则底面圆的半径$r$为
3
cm.
答案:
12.3
13. 如图,点O是$\triangle PMN$的内心,$PO$的延长线和$\triangle PMN$的外接圆相交于点Q,连接$NQ$,$MO$,$NO$. 若$\angle MNQ = 15^{\circ}$,则$\angle MON$的度数为
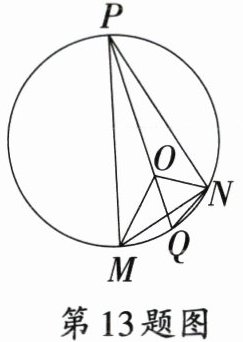
105°
.
答案:
13.105° [解析]
∵点O是△PMN的内心,
∴PQ平分∠MPN,MO平分∠PMN,NO平分∠PNM.
∴∠MPQ = ∠NPQ,∠OMN = $\frac{1}{2}$∠PMN,∠ONM = $\frac{1}{2}$∠PNM.
∵∠MNQ = 15°,
∴∠NPQ = ∠MPQ = ∠MNQ = 15°.
∴∠MPN = 30°.
∴∠PMN + ∠PNM = 150°.
∴∠OMN + ∠ONM = $\frac{1}{2}$(∠PMN + ∠PNM) = 75°.
∴∠MON = 180° - (∠OMN + ∠ONM) = 105°.
∵点O是△PMN的内心,
∴PQ平分∠MPN,MO平分∠PMN,NO平分∠PNM.
∴∠MPQ = ∠NPQ,∠OMN = $\frac{1}{2}$∠PMN,∠ONM = $\frac{1}{2}$∠PNM.
∵∠MNQ = 15°,
∴∠NPQ = ∠MPQ = ∠MNQ = 15°.
∴∠MPN = 30°.
∴∠PMN + ∠PNM = 150°.
∴∠OMN + ∠ONM = $\frac{1}{2}$(∠PMN + ∠PNM) = 75°.
∴∠MON = 180° - (∠OMN + ∠ONM) = 105°.
14.[兰州中考] “轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,图1是陈列在展览馆的仿真模型. 图2是模型驱动部分的示意图,其中⊙M,⊙N的半径分别是1 cm和10 cm,当⊙M顺时针转动3周时,⊙N上的点P随之旋转$n^{\circ}$,则$n =$
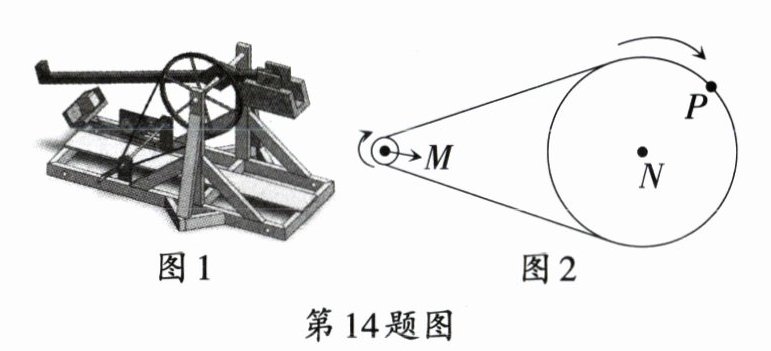
108
.
答案:
14.108
查看更多完整答案,请扫码查看


