《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

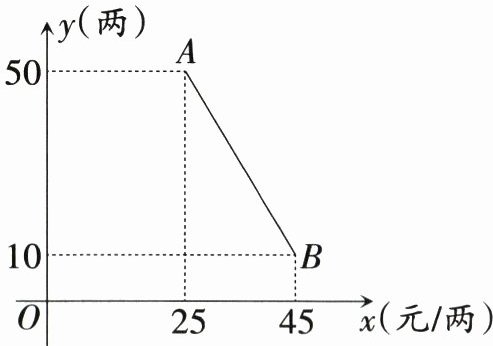
21. 〔郑州市改编〕(10分)巩义特产小相菊花茶深受顾客喜爱，小相菊花茶进价为20元/两，某商店对销售情况进行了调查，结果发现月最大销售量$y$(两)与售价$x$(元/两)($25 \leq x \leq 45$)之间的函数关系如图中的线段$AB$所示.(月最大销售量指进货量足够的情况下最多售出数量)
(1)求出$y$与$x$之间的函数解析式.
(2)若该菊花茶某月的总销售利润为$w$元，求$w$关于$x$的函数解析式.当售价$x$为多少元/两时，销售利润$w$最大？

答案： 21.解：
(1)设$y$与$x$的函数解析式为$y = kx + b$。
将点$(25,50)$，$(45,10)$代入$y = kx + b$，
得$\begin{cases}25k + b = 50\\45k + b = 10\end{cases}$解得$\begin{cases}k = -2\\b = 100\end{cases}$
∴$y$与$x$之间的函数解析式为$y=-2x + 100$。
(2)根据题意，得$w = y(x - 20)=(-2x + 100)·(x - 20)=-2(x - 35)^{2}+450$。
∵$25\leq x\leq45$，$-2＜0$，
∴当$x = 35$时，$w$取得最大值。
∴当售价$x$为$35$元/两时，销售利润$w$最大。

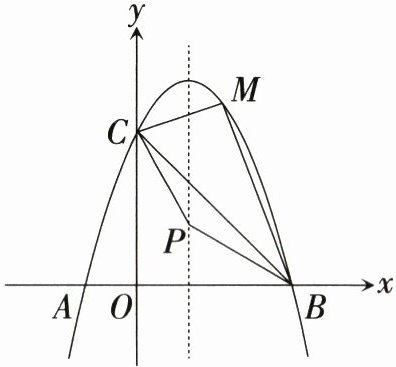
22. (10分)如图，抛物线$y = -x^2 + bx + c$过点$A(-1, 0)$，$B(3, 0)$，与$y$轴交于点$C$.
(1)求抛物线的解析式.
(2)$P$为抛物线对称轴上一动点，当$\triangle PCB$是以$BC$为底边的等腰三角形时，求点$P$的坐标.
(3)在(2)的条件下，是否存在$M$为抛物线第一象限内的一点，使得$S_{\triangle BCM} = S_{\triangle BCP}$？若存在，求出点$M$的横坐标；若不存在，请说明理由.

答案：
22.解：
(1)将$A(-1,0)$，$B(3,0)$代入$y=-x^{2}+bx + c$，
得$\begin{cases}-1 - b + c = 0\\-9 + 3b + c = 0\end{cases}$解得$\begin{cases}b = 2\\c = 3\end{cases}$
∴抛物线的解析式为$y=-x^{2}+2x + 3$。
(2)
∵抛物线的解析式为$y=-x^{2}+2x + 3$，
∴抛物线的对称轴为直线$x = 1$。记对称轴与$x$轴交点为$D$，
∴$OD = 1$。
令$x = 0$，得$y = 3$。
∴点$C(0,3)$。
∴$OB = OC = 3$。
∴$\triangle BOC$为等腰直角三角形。
∵当$\triangle PCB$是以$BC$为底边的等腰三角形时，有$PB = PC$，
∴此时点$P$为$BC$的垂直平分线上的点，连接$OP$，则$OP$平分$\angle BOC$。
∴$\angle BOP=\frac{1}{2}\angle BOC = 45^{\circ}$。
∴$\angle OPD=\angle BOP = 45^{\circ}$。
∵$P$为抛物线对称轴上的点，
∴$PD = OD = 1$。
∴点$P$的坐标为$(1,1)$。
(3)存在。
如图，过点$P$作$PQ// BC$交$y$轴于点$Q$，过点$M$作
$MN// BC$交$y$轴于点$N$。

设直线$BC$的解析式为$y = mx + n$，将点$B(3,0)$，
$C(0,3)$代入，得$\begin{cases}3m + n = 0\\n = 3\end{cases}$解得$\begin{cases}m = -1\\n = 3\end{cases}$
∴直线$BC$的解析式为$y=-x + 3$。
∵$PQ// BC$，
∴设直线$PQ$的解析式为$y=-x + q$。将点$P(1,1)$代入，得$q = 2$。
∴直线$PQ$的解析式为$y=-x + 2$。
令$x = 0$，得$y = 2$。
∴点$Q(0,2)$。
∵$S_{\triangle BCM}=S_{\triangle BCP}$，
∴直线$PQ$，$MN$到直线$BC$的距离相等。
∵点$C(0,3)$，
∴由平移的性质可知，点$N(0,4)$。
∴直线$MN$的解析式为$y=-x + 4$。
令$-x^{2}+2x + 3=-x + 4$，
解得$x_{1}=\frac{3 + \sqrt{5}}{2}$，$x_{2}=\frac{3 - \sqrt{5}}{2}$。
∴点$M$的横坐标为$\frac{3 + \sqrt{5}}{2}$或$\frac{3 - \sqrt{5}}{2}$。