《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

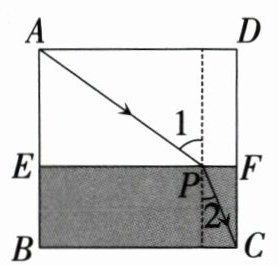
15. 跨学科 物理 如图，小明利用折射定律$n_1 · \sin\alpha = n_2 · \sin\beta$($n_1$，$n_2$为折射率，$\angle \alpha$为入射角，$\angle \beta$为折射角)制作了一个测算某液体折射率的装置，光线从点$A$按固定角度从空气射入液体，通过调节液面高度，使光线折射后恰好落到点$C$.已知$\sin\angle 1 = \frac{4}{5}$，空气折射率$n_1$为$1$，正方形$ABCD$的边长为$36\ cm$ ($\angle 1$为入射角，$\angle 2$为折射角).若$CF = 15\ cm$，则$\sin\angle EAP =$ $\frac{4}{5}$，该液体的折射率为$\frac{17}{10}$.

答案： 15.$\frac{4}{5}$　$\frac{17}{10}$　[解析]根据题意,得AB=BC=36cm,四边形BCFE为矩形.
∴EF=BC=36cm.设法线为l.
∵AB//CD//l,
∴∠1=∠EAP,∠2=∠PCF.
∵sin∠1=$\frac{4}{5}$,
∴sin∠EAP=$\frac{EP}{AP}$=$\frac{4}{5}$设EP=4xcm,则AP=5xcm.
∴AE=3xcm.
∴题图中PF=EF −EP=(36−4x)cm,CF=BE=AB−AE=(36−3x)cm.
∵CF=15cm,
∴36−3x=15.解得x=7.
∴PF=8cm.
∴CP=$\sqrt{CF²+PF²}$=17cm.
∴sin∠2=sin∠PCF=$\frac{PF}{CP}$=$\frac{8}{17}$
∵n₁·sin∠1=n₂·sin∠2,
∴$\frac{4}{5}$×1=$\frac{8}{17}$n₂.
∴n₂=$\frac{17}{10}$.

16. (10分)计算：(1)$\sin 30^{\circ} + \tan^2 45^{\circ} - \cos 45^{\circ} · \tan 60^{\circ}$；
(2)$\frac{\sqrt{2}}{4} \sin 45^{\circ} + \cos^2 30^{\circ} - \frac{1}{2 \tan 60^{\circ}} + 2 \sin 60^{\circ}$.

答案： 16.解:
(1)原式=$\frac{1}{2}$+1−$\frac{\sqrt{2}}{2}$×$\sqrt{3}$　(3分)
　　=$\frac{3}{2}$−$\frac{\sqrt{6}}{2}$.　(5分)
(2)原式=$\frac{\sqrt{2}}{4}$×$\frac{\sqrt{2}}{2}$ + $(\frac{\sqrt{3}}{2})^2$−$\frac{1}{2×\sqrt{3}}$+2×$\frac{\sqrt{3}}{2}$　(3分)
　　=$\frac{1}{4}$+$\frac{3}{4}$−$\frac{\sqrt{3}}{6}$+$\sqrt{3}$
　　=1+$\frac{5\sqrt{3}}{6}$.　(5分)

17. ［郑州模拟］(8分)先化简，再求值：$\left( \frac{2x - 1}{x + 1} - x + 1 \right) ÷ \frac{x - 2}{x^2 + 2x + 1}$，其中$x = \sqrt{2} + 2\cos 60^{\circ}$.

答案： 17.解:原式=$\frac{2x - 1 - x^{2} + 1}{(x + 1)(x - 2)} = \frac{-x(x - 2)}{(x + 1)(x - 2)} = - \frac{x}{x + 1} = - x(x + 1) = - x^{2} - x$.(4分)
当$x = \sqrt{2} + 2\cos60^{\circ} = \sqrt{2} + 2 × \frac{1}{2} = \sqrt{2} + 1$时，
原式$= - (\sqrt{2} + 1)^{2} - (\sqrt{2} + 1) = - 3\sqrt{2} - 4$.(8分)