2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
23.[郑州外国语中学] (11分)如图,AB是⊙O的直径,$PC$切⊙O于点P,过点A作直线$AC\bot PC$交⊙O于另一点D,连接PA,PB,PO.
(1)求证:$AP$平分$\angle CAB$.
(2)若P是直径AB上方圆弧上一动点,⊙O的半径为2,则:
①当$\overset{\frown}{AP}$的长是
②当弦AP的长度是
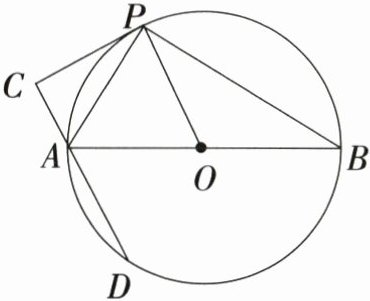
(1)求证:$AP$平分$\angle CAB$.
(2)若P是直径AB上方圆弧上一动点,⊙O的半径为2,则:
①当$\overset{\frown}{AP}$的长是
$\pi$
时,以A,O,P,C为顶点的四边形是正方形;②当弦AP的长度是
2或$2\sqrt{3}$
时,以A,D,O,P为顶点的四边形是菱形.
答案:
23.解:
(1)证明:
∵PC切⊙O于点P,
∴∠OPC = 90°.
∵AC⊥PC,
∴∠C = 90°.
∴∠OPC + ∠C = 180°.
∴AC//OP.
∴∠CAP = ∠APO.
∵OP = OA,
∴∠OAP = ∠APO.
∴∠OAP = ∠CAP.
∴AP平分∠CAB.(5分)
(2)①$\pi$
②2或$2\sqrt{3}$(11分)
[解析]①当以A,O,P,C为顶点的四边形为正方形时,∠AOP = 90°,AP的长为$\frac{90\pi×2}{180}$ = $\pi$.
②连接OD.根据题意,分两种情况:I.当AP为边时,如图①所示.当四边形ADOP是菱形时,AP = OP = OD = AD.
∴AP = OP = 2.
II.当AP为对角线时,如图②所示.当四边形ADPO是菱形时,OA = OP = PD = AD.
∴OA = OD = AD.
∴△AOD为等边三角形.
∴∠AOD = 60°.
设AP与OD的交点为G.
则AP = 2AG,∠AGO = 90°.
∴∠OAG = 90° - ∠AOD = 30°,
∴OG = $\frac{1}{2}$OA = 1.
∴AG = $\sqrt{OA^{2}-OG^{2}}$ = $\sqrt{3}$.
∴AP = $2\sqrt{3}$.
综上所述,当弦AP的长度是2或$2\sqrt{3}$时,以A,D,O,P为顶点的四边形是菱形.


23.解:
(1)证明:
∵PC切⊙O于点P,
∴∠OPC = 90°.
∵AC⊥PC,
∴∠C = 90°.
∴∠OPC + ∠C = 180°.
∴AC//OP.
∴∠CAP = ∠APO.
∵OP = OA,
∴∠OAP = ∠APO.
∴∠OAP = ∠CAP.
∴AP平分∠CAB.(5分)
(2)①$\pi$
②2或$2\sqrt{3}$(11分)
[解析]①当以A,O,P,C为顶点的四边形为正方形时,∠AOP = 90°,AP的长为$\frac{90\pi×2}{180}$ = $\pi$.
②连接OD.根据题意,分两种情况:I.当AP为边时,如图①所示.当四边形ADOP是菱形时,AP = OP = OD = AD.
∴AP = OP = 2.
II.当AP为对角线时,如图②所示.当四边形ADPO是菱形时,OA = OP = PD = AD.
∴OA = OD = AD.
∴△AOD为等边三角形.
∴∠AOD = 60°.
设AP与OD的交点为G.
则AP = 2AG,∠AGO = 90°.
∴∠OAG = 90° - ∠AOD = 30°,
∴OG = $\frac{1}{2}$OA = 1.
∴AG = $\sqrt{OA^{2}-OG^{2}}$ = $\sqrt{3}$.
∴AP = $2\sqrt{3}$.
综上所述,当弦AP的长度是2或$2\sqrt{3}$时,以A,D,O,P为顶点的四边形是菱形.


查看更多完整答案,请扫码查看


