《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

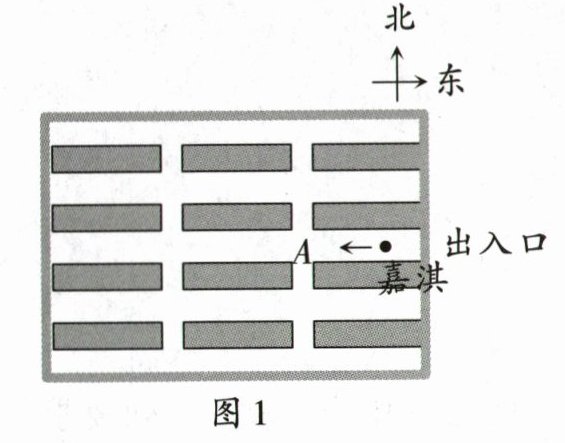
19. 〔河北中考〕(9分)某博物馆展厅的俯视示意图如图1所示.嘉淇进入展厅后开始自由参观,每走到一个十字道口,他自己可能直行,也可能向左转或向右转,且这三种可能性均相同.
(1) 求嘉淇走到十字道口$A$向北走的概率;
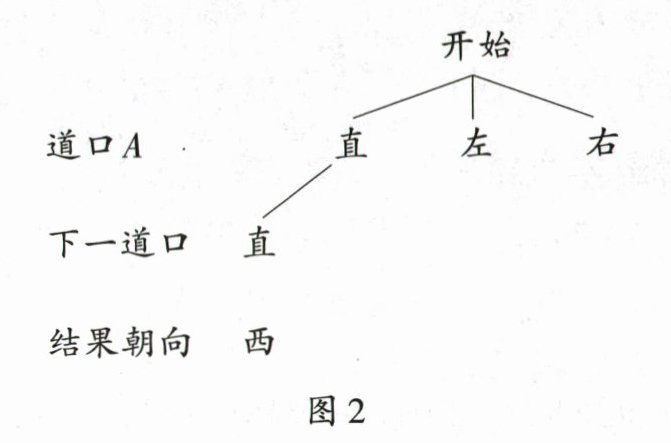
(2) 补全图2的树状图,并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大.

答案：
19.解：
(1)根据题意，得共有$3$种等可能的结果，向北走只有$1$种结果，
$\therefore P($嘉淇向北走$)=\frac{1}{3}$。(3分)
(2)补全的树状图如图。
道口$A$

下一道口
结果朝向 西南北 南东西 西北西 东(6分)
由树状图可知，共有$9$种等可能的结果，其中向东参观有$2$种，向西参观有$3$种，向南参观有$2$种，向北参观有$2$种。
$\therefore P($向西参观$)=\frac{3}{9}=\frac{1}{3}$，$P($向东参观$)=P($向南参观$)=P($向北参观$)=\frac{2}{9}$。
$\because\frac{1}{3}＞\frac{2}{9}$，$\therefore$嘉淇经过两个十字道口后向西参观的概率较大。(9分)

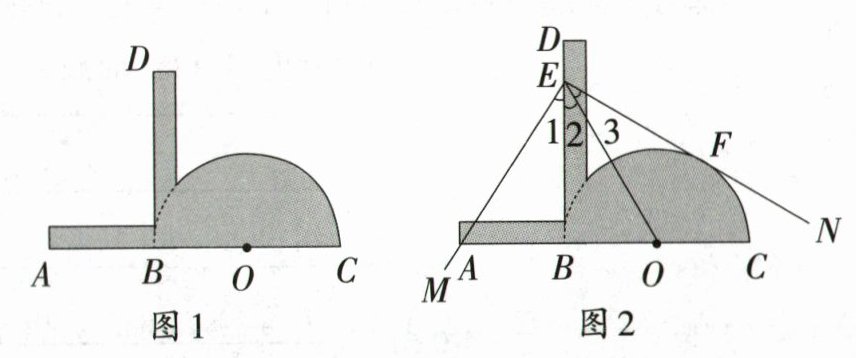
20. 〔河南中考〕(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图1是它的示意图,其中$AB$与半圆$O$的直径$BC$在同一直线上,且$AB$的长度与半圆$O$的半径相等;$DB$与$AC$垂直于点$B$,$DB$足够长.
使用方法如图2所示,若要把$\angle MEN$三等分,只需适当放置三分角器,使$DB$经过$\angle MEN$的顶点$E$,点$A$落在边$EM$上,半圆$O$与另一边$EN$恰好相切,切点为$F$,则$EB,EO$就把$\angle MEN$三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点$A,B,O,C$在同一直线上,$EB\perp AC$,垂足为点$B$,AB = OB，点A落在边EM上，EN切半圆O于点F.
求证:$\angle1=\angle2=\angle3$.

答案： 20.解：补充如下。已知：$AB = OB$，点$A$落在边$EM$上，$EN$切半圆$O$于点$F$(2分)
求证：$\angle1=\angle2=\angle3$(4分)
证明：连接$OF$。$\because EB\perp AC$，
$\therefore\angle ABE=\angle OBE = 90^{\circ}$。
$\because AB = OB$，$EB = EB$，
$\therefore\triangle ABE\cong\triangle OBE$。(6分)
$\therefore\angle1=\angle2$。
$\because EN$切半圆$O$于点$F$，$\therefore OF\perp EF$。
$\because OB\perp EB$且$OF = OB$，
$\therefore EO$平分$\angle BEF$。
$\therefore\angle3=\angle2$。$\therefore\angle1=\angle2=\angle3$。(9分)