《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

23. 〔郑州市〕(11分)综合与实践.
【问题发现】有这样一个问题：如图1，已知正方形$ABCD$，$E$为对角线$AC$上一动点，过点$C$作垂直于$AC$的射线$CG$，点$F$在射线$CG$上，且$\angle EBF = 90^{\circ}$，连接$EF$.
通过观察图形，数学兴趣小组的同学进行了如下猜想：
猜想①：$BE = BF$；
猜想②：$AE = CF$；
猜想③：点$E$在$AC$上运动的过程中，四边形$BECF$的面积不变.
(1)上述猜想中正确的有①②③(填序号).
【类比探究】
(2)兴趣小组的同学在探究了正方形中的结论后，将正方形换成矩形继续探究.如图2，已知矩形$ABCD$，$AB = 8$，$AD = 4$，$E$为对角线$AC$上一动点，过点$C$作垂直于$AC$的射线$CG$，点$F$在射线$CG$上，且$\angle EBF = 90^{\circ}$，连接$EF$.
①请判断线段$AE$与$CF$的数量关系，并说明理由；
②点$E$在$AC$上运动时，四边形$BECF$的面积改变(选填“不变”或“改变”).
【拓展应用】
(3)在(2)的条件下，点$E$在对角线$AC$上运动，当四边形$BECF$为轴对称图形时，请直接写出线段$BF$的长.

答案：
23.解:
(1)①②③　　　　　　　　　　　　　(3分)
[解析]
∵四边形ABCD是正方形，
∴AB=BC,∠ABC=90°,∠BAE=∠BCE=45°.
∵∠EBF=90°,
∴∠ABC=∠EBF,即∠ABE+∠EBC=∠EBC +∠CBF.
∴∠ABE=∠CBF.
∵AC⊥CG,
∴∠ECF=90°.
∵∠BCE=45°,
∴∠BCF=45°.
∴∠BAE=∠BCF.
∴△ABE≌△CBF.
∴BE=BF,AE=CF.猜想①、猜想②正确.
∵△ABE≌△CBF,
∴S△ABE=S△CBF.
∴S四边形BECF=S△BEC+S△CBF=S△BEC+S△ABE=S△ABC.
∴点E在AC上运动的过程中，四边形BECF的面积不变.猜想③正确.综上所述，猜想①猜想②、猜想③均正确.
(2)①AE=2CF.　　　　　　　　　　　　　(4分)
理由:
∵四边形ABCD是矩形，
∴∠ABC=90°,BC=AD=4.
∴$\frac{AB}{BC}$=2,∠BCE+∠BAE=90°.
∵∠EBF=90°,
∴∠ABC=∠EBF,
即∠ABE+∠EBC=∠EBC+∠CBF.
∴∠ABE=∠CBF,
∵AC⊥CG,
∴∠ECF=90°.
∴∠BCF+∠BCE=∠BCE+∠BAE.
∴∠BAE=∠BCF.
∴△ABE∽△CBF.
∴$\frac{AE}{CF}$=$\frac{AB}{BC}$=2.
∴AE=2CF.　　　　　　(7分)
②改变　　　　　　　　　　　　　　　　　(9分)
(3)线段BF的长为$\sqrt{5}$或$\frac{4\sqrt{5}}{5}$.　　　　　(11分)
[解析]
∵在Rt△ABC中,AB=8,BC=4,
∴AC=$\sqrt{AB²+BC²}$=4$\sqrt{5}$.
与
(2)①同理可得,△ABE∽△CBF.
∴$\frac{BE}{BF}$=$\frac{AB}{BC}$=2,即BF=$\frac{1}{2}$BE.
由题可知，分两种情况:
a.当四边形BECF关于EF所在直线对称时，如图①,设EF交BC于点H.

　
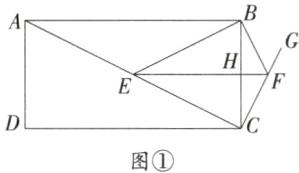
∴EF垂直平分BC.
∴$\frac{BH}{BC}$=$\frac{1}{2}$.
∵AB⊥BC,
∴AB//EF.
∴$\frac{AE}{AC}$=$\frac{BH}{BC}$=$\frac{1}{2}$.
∴点E为AC的中点.
∴BE=$\frac{1}{2}$AC=2$\sqrt{5}$.
∴BF=$\sqrt{5}$.
b.当四边形BECF为矩形时,如图②.

∴∠BEC=90°.
∴S△ABC=$\frac{1}{2}$AB·BC=$\frac{1}{2}$AC·BE.
∴BE=$\frac{AB·BC}{AC}$=$\frac{8\sqrt{5}}{5}$.
∴BF=$\frac{4\sqrt{5}}{5}$.
综上所述，线段BF的长为$\sqrt{5}$或$\frac{4\sqrt{5}}{5}$.