《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

9. 〔天津市〕已知抛物线$y = x^2 + 2mx + m - 7$与$x$轴的两个交点在点$(1, 0)$两旁，则关于$x$的方程$\frac{1}{4}x^2 + (m + 1)x + m^2 + 5 = 0$的根的情况是 (D)

A.有两个不相等的实数根
B.有两个相等的实数根
C.有实数根
D.无实数根

答案： 9.D [解析]
∵抛物线$y=x^{2}+2mx+m - 7$与$x$轴的两个交点在点$(1,0)$两旁，
∴当$x = 1$时，$y=1 + 2m + m - 7＜0$。解得$m ＜ 2$。
∵方程$\frac{1}{4}x^{2}+(m + 1)x + m^{2}+5 = 0$，
∴$\Delta=(m + 1)^{2}-4×\frac{1}{4}×(m^{2}+5)=2m - 4＜0$。
∴方程$\frac{1}{4}x^{2}+(m + 1)x + m^{2}+5 = 0$无实数根。故选D。

10. 〔南阳市〕如图，在等边三角形$ABC$中，$AB = 2$，点$D$从点$A$出发，以每秒2个单位长度的速度沿折线$A—C—B$运动，过点$D$作$AB$的垂线，垂足为点$E$. 设点$D$的运动时间为$x$ s，$\triangle ADE$的面积为$y$(当$A$，$D$，$E$三点共线时，不妨设$y = 0$)，则能够反映$y$与$x$之间的函数关系的图象是 (C)

A
B
C
D

答案： 10.C

11. 设题新角度 开放性试题 请写出一个开口向上且经过$( - 2, 0)$的抛物线的解析式：$y = x^{2}-4$.

答案： 11.$y = x^{2}-4$(答案不唯一)

12. 〔武汉市〕飞机着陆后滑行的距离$s$(单位：m)与滑行的时间$t$(单位：s)之间的函数关系式为$s = 96t - 1.2t^2$，那么飞机着陆后滑行1920m停下.

答案： 12.1920

13. 已知函数$y = \begin{cases}-x^2 + 2x, & (x ＞ 0) \\ -x, & (x \leq 0)\end{cases}$的图象如图所示，若直线$y = m$与该图象恰有两个不同的交点，则$m$的值为 ______ .

答案： 13.0或1 [解析]
∵$y=-x^{2}+2x=-(x - 1)^{2}+1$，
∴当$x＞0$时，二次函数图象的顶点为$(1,1)$。由图象可知，当$m = 0$或$m = 1$时，直线$y = m$与该图象恰有两个不同的交点。

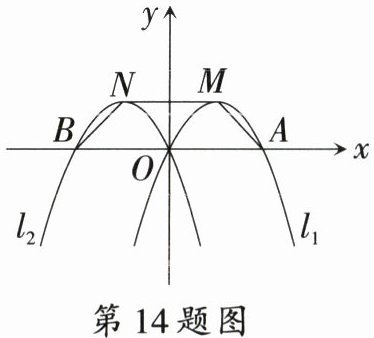
14. 如图，已知抛物线$l_1: y = -x^2 + 2x$与$x$轴分别交于$A$，$O$两点，顶点为$M$. 将抛物线$l_1$关于$y$轴对称得到抛物线$l_2$，则抛物线$l_2$过点$O$，与$x$轴的另一个交点为$B$，顶点为$N$，连接$AM$，$MN$，$NB$，则四边形$AMNB$的面积为3.

答案： 14.3 [解析]过点$N$作$NC\perp AB$交$AB$于点$C$。
∵抛物线$l_{1}$的解析式为$y=-x^{2}+2x=-(x - 1)^{2}+1$，
∴抛物线$l_{1}$的顶点坐标为$M(1,1)$。当$y = 0$时，$-x^{2}+2x = 0$，解得$x_{1}=0$，$x_{2}=2$。
∴点$A$的坐标为$(2,0)$。
∵$l_{2}$和$l_{1}$关于$y$轴对称，
∴点$N$和点$M$关于$y$轴对称，点$B$和点$A$关于$y$轴对称。
∴$N(-1,1)$，$B(-2,0)$。
∵$MN// AB$，
∴四边形$AMNB$是梯形。
∵$MN = 1-(-1)=2$，$AB = 2-(-2)=4$，$NC = 1$，
∴$S_{四边形AMNB}=\frac{1}{2}(MN + AB)· NC = 3$。

15. 二次函数$y = ax^2 + bx + c(a \neq 0)$的图象如图所示，下列结论：①$abc ＞ 0$；②$2a + b = 0$；③当$m \neq 1$时，$a + b ＞ am^2 + bm$；④$a - b + c ＞ 0$；⑤若$ax_1^2 + bx_1 = ax_2^2 + bx_2$，且$x_1 \neq x_2$，则$x_1 + x_2 = 2$.其中正确的有②③⑤.(填序号)

答案： 15.②③⑤ [解析]
∵抛物线的开口向下，
∴$a＜0$。
∵抛物线的对称轴为直线$x =-\frac{b}{2a}=1$，
∴$b=-2a$。
∴$b＞0$。
∵抛物线与$y$轴的交点在$x$轴上方，
∴$c＞0$。
∴$abc＜0$。①错误。
∵$b=-2a$，
∴$2a + b = 0$。②正确。
∵$x = 1$时，函数值最大，
∴当$m\neq1$
时，$a + b + c＞am^{2}+bm + c$，即$a + b＞am^{2}+bm$。
③正确。由图象可知，当$x = 3$时，$y＜0$。
∵抛物线的对称轴为直线$x = 1$，
∴$x=-1$和$x = 3$所对应的函数值相等。
∴当$x=-1$时，$y＜0$。
∴$a - b + c＜0$。
④错误。若$ax_{1}^{2}+bx_{1}=ax_{2}^{2}+bx_{2}$，则$ax_{1}^{2}+bx_{1}+c=ax_{2}^{2}+bx_{2}+c$。
∵$x_{1}\neq x_{2}$，
∴$x = x_{1}$和$x = x_{2}$所对应的函数值相等。
∴$\frac{x_{1}+x_{2}}{2}=1$。
∴$x_{1}+x_{2}=2$。
⑤正确。综上所述，正确的有②③⑤。