2026年王朝霞考点梳理时习卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年王朝霞考点梳理时习卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
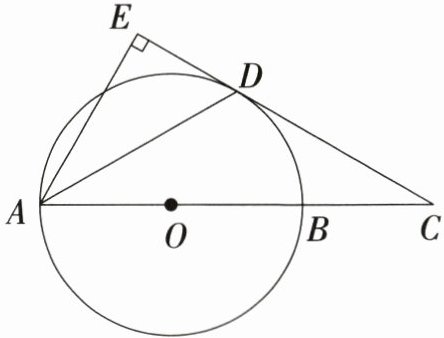
21. 课后题改编 (10分)如图,AB是⊙O的直径,点C在AB的延长线上,$AD$平分$\angle CAE$交⊙O于点D,且$AE\bot CD$,垂足为点E.
(1)判断直线CE与⊙O的位置关系,并说明理由;
(2)若$BC = 3$,$CD = 3\sqrt{3}$,求ED的长.
(1)判断直线CE与⊙O的位置关系,并说明理由;
(2)若$BC = 3$,$CD = 3\sqrt{3}$,求ED的长.

答案:
21.解:
(1)CE与⊙O相切.
理由如下:连接OD.
∵OA = OD,
∴∠OAD = ∠ODA.
∵AD平分∠CAE,
∴∠EAD = ∠OAD.
∴∠EAD = ∠ODA.
∴OD//AE.
∵AE⊥CD,
∴OD⊥CD.
∵OD是⊙O的半径,
∴CE是⊙O的切线,即CE与⊙O相切.(5分)
(2)连接OD,BD.设OD = OB = x.
∵在Rt△COD中,$CD = 3\sqrt{3}$,
∴由勾股定理,得$OD^{2}+CD^{2}=OC^{2}$,
即$x^{2}+(3\sqrt{3})^{2}=(x + 3)^{2}$.解得x = 3.
∴OD = OB = 3.
∴OB = BC.
∴BD = OB.
∴△OBD为等边三角形.
∴∠BOD = 60°.
∴∠C = 90° - ∠BOD = 30°,
∠OAD = $\frac{1}{2}$∠BOD = 30°.
∴∠C = ∠OAD,∠EAD = ∠OAD = 30°.
∴AD = CD = $3\sqrt{3}$.
∴ED = $\frac{1}{2}$AD = $\frac{3\sqrt{3}}{2}$.(10分)
(1)CE与⊙O相切.
理由如下:连接OD.
∵OA = OD,
∴∠OAD = ∠ODA.
∵AD平分∠CAE,
∴∠EAD = ∠OAD.
∴∠EAD = ∠ODA.
∴OD//AE.
∵AE⊥CD,
∴OD⊥CD.
∵OD是⊙O的半径,
∴CE是⊙O的切线,即CE与⊙O相切.(5分)
(2)连接OD,BD.设OD = OB = x.
∵在Rt△COD中,$CD = 3\sqrt{3}$,
∴由勾股定理,得$OD^{2}+CD^{2}=OC^{2}$,
即$x^{2}+(3\sqrt{3})^{2}=(x + 3)^{2}$.解得x = 3.
∴OD = OB = 3.
∴OB = BC.
∴BD = OB.
∴△OBD为等边三角形.
∴∠BOD = 60°.
∴∠C = 90° - ∠BOD = 30°,
∠OAD = $\frac{1}{2}$∠BOD = 30°.
∴∠C = ∠OAD,∠EAD = ∠OAD = 30°.
∴AD = CD = $3\sqrt{3}$.
∴ED = $\frac{1}{2}$AD = $\frac{3\sqrt{3}}{2}$.(10分)
22.[安阳市] (10分)阅读材料,解答问题:
关于圆的引理古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题.
如图1,AB是⊙O的弦,点C在⊙O上,$CD\bot AB$于点D,在弦AB上取点E,使$DE = AD$,点F是$\overset{\frown}{BC}$上的一点,且$\overset{\frown}{CF} = \overset{\frown}{CA}$,连接BF,则$BF = BE$.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC.
$\because CD\bot AB$,$DE = AD$,
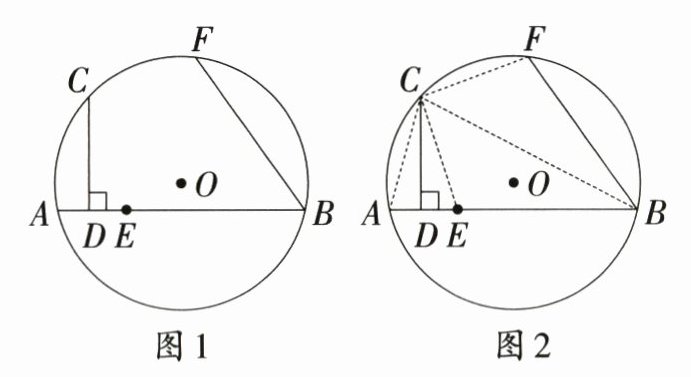
$\therefore CA = CE$.
$\therefore \angle CAE = \angle CEA$.
$\because \overset{\frown}{CF} = \overset{\frown}{CA}$,
$\therefore CF = CA$(依据1),$ \angle CBF = \angle CBA$.
$\because$四边形ABFC内接于⊙O,
$\therefore \angle CAB + \angle CFB = 180^{\circ}$(依据2).
$\ldots \ldots$
(1)上述证明过程中的依据1为
(2)将上述证明过程补充完整.
关于圆的引理古希腊数学家、物理学家阿基米德流传于世的数学著作有10余种,下面是《阿基米德全集》的《引理集》中记载的一个命题.
如图1,AB是⊙O的弦,点C在⊙O上,$CD\bot AB$于点D,在弦AB上取点E,使$DE = AD$,点F是$\overset{\frown}{BC}$上的一点,且$\overset{\frown}{CF} = \overset{\frown}{CA}$,连接BF,则$BF = BE$.
小颖对这个问题很感兴趣,经过思考,写出了下面的证明过程:
证明:如图2,连接CA,CE,CF,BC.
$\because CD\bot AB$,$DE = AD$,

$\therefore CA = CE$.
$\therefore \angle CAE = \angle CEA$.
$\because \overset{\frown}{CF} = \overset{\frown}{CA}$,
$\therefore CF = CA$(依据1),$ \angle CBF = \angle CBA$.
$\because$四边形ABFC内接于⊙O,
$\therefore \angle CAB + \angle CFB = 180^{\circ}$(依据2).
$\ldots \ldots$
(1)上述证明过程中的依据1为
在同圆中,如果两条弧相等,那么它们所对的弦相等
,依据2为圆内接四边形的对角互补
;(2)将上述证明过程补充完整.
答案:
22.解:
(1)在同圆中,如果两条弧相等,那么它们所对的弦相等 圆内接四边形的对角互补 (6分)
(2)
∵∠CEA + ∠CEB = 180°,
∴∠CFB = ∠CEB.
∵BC = BC,
∴△CFB≌△CEB.
∴BF = BE.(10分)
(1)在同圆中,如果两条弧相等,那么它们所对的弦相等 圆内接四边形的对角互补 (6分)
(2)
∵∠CEA + ∠CEB = 180°,
∴∠CFB = ∠CEB.
∵BC = BC,
∴△CFB≌△CEB.
∴BF = BE.(10分)
查看更多完整答案,请扫码查看


