《2026年王朝霞考点梳理时习卷九年级数学全一册人教版》

16. (10分)解下列方程.
(1) $(x+3)^2=4(x-3)^2$;
(2) $x(5x-3)=1-7x$.

答案： 16.解：
(1)两边开平方，得$x + 3=\pm2(x - 3)$。(2分)
$\therefore x + 3 = 2(x - 3)$或$x + 3=-2(x - 3)$。(4分)
解得$x_{1}=9$，$x_{2}=1$。(5分)
(2)将原方程化简，得$5x^{2}+4x - 1 = 0$。
$\therefore(5x - 1)(x + 1)=0$。(2分)
$\therefore5x - 1 = 0$或$x + 1 = 0$。(4分)
解得$x_{1}=\frac{1}{5}$，$x_{2}=-1$。(5分)

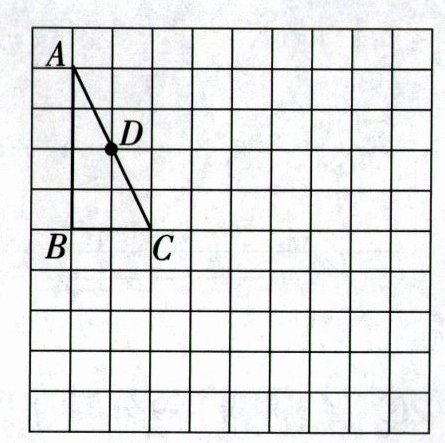
17. 〔南阳市〕(8分)如图,在$\triangle ABC$中,$\angle B=90°$,$D$为边$AC$的中点.请按下列要求作图,并解决问题:
(1) 作点$D$关于$BC$的对称点$O$.
(2) 在(1)的条件下,将$\triangle ABC$绕点$O$顺时针旋转$90°$.
① 画出旋转后的$\triangle EFG$(其中$A,B,C$三点旋转后的对应点分别是点$E,F,G$);
② $\angle BOF=$90度,若$\angle ACB=\alpha$,则$\angle FEG=$$90^{\circ}-\alpha$(用含$\alpha$的式子表示).

答案：
17.解：
(1)点$O$如图所示。(3分)

(2)①$\triangle EFG$如图所示。(6分)
②$90$ $90^{\circ}-\alpha$(8分)

18. 〔长春市〕(9分)在平地上抛掷一枚图钉,通常会出现两种情况:
(钉尖着地)
(钉尖不着地)
下面是小明和同学做“抛掷图钉试验”获得的数据:

(1) 填写表中的空格;
(2) 画出该试验中抛掷图钉“钉尖不着地”的频率折线统计图;

(3) 根据“抛掷图钉试验”的结果,估计“钉尖着地”的概率为0.39.

答案：
18.解：
(1)$0.62$ $0.62$ $0.61$(3分)
(2)如图所示。
(6分)
(3)$0.39$(9分)
[解析]通过大量试验，发现图钉“钉尖不着地”的频率围绕$0.61$上下波动，$\therefore$估计图钉“钉尖不着地”的概率为$0.61$。$\therefore$估计“钉尖着地”的概率$P = 1 - 0.61 = 0.39$。